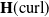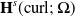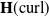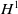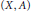Refine search
Actions for selected content:
2 results
Solving two-dimensional H(curl)-elliptic interface systems with optimal convergence on unfitted meshes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 774-805
-
- Article
- Export citation
Relative Homotopy in Relational Structures
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 2 / 01 June 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-320
- Print publication:
- 01 June 2008
-
- Article
-
- You have access
- Export citation