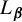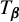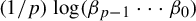Refine search
Actions for selected content:
89 results
Reconciling the social and spatial: An apparent-time analysis of variation intensity in colloquial German
-
- Journal:
- Journal of Linguistic Geography , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 93-127
- Print publication:
- January 2026
-
- Article
- Export citation
(Almost) complete characterization of the stability of a discrete-time Hawkes process with inhibition and memory of length two
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1463-1484
- Print publication:
- December 2024
-
- Article
- Export citation

Economic Networks
- Theory and Computation
-
- Published online:
- 11 April 2024
- Print publication:
- 25 April 2024
LIMIT SETS OF UNFOLDING PATHS IN OUTER SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2365-2403
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximation with ergodic processes and testability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 January 2024, pp. 1040-1059
- Print publication:
- September 2024
-
- Article
- Export citation
Comparison theorem and stability under perturbation of transition rate matrices for regime-switching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 14 September 2023, pp. 540-557
- Print publication:
- June 2024
-
- Article
- Export citation
1 - Geometric Measure Theory
- from Part I - Ergodic Theory and Geometric Measures
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 3-54
-
- Chapter
- Export citation
20 - Sullivan h-Conformal Measures for Compactly Nonrecurrent Elliptic Functions
- from Part VI - Compactly Nonrecurrent Elliptic Functions: Fractal Geometry, Stochastic Properties, and Rigidity
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 307-334
-
- Chapter
- Export citation
Strong feller and ergodic properties of the (1+1)-affine process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 March 2023, pp. 812-834
- Print publication:
- September 2023
-
- Article
- Export citation
On the ergodicity of geodesic flows on surfaces without focal points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 4226-4248
- Print publication:
- December 2023
-
- Article
- Export citation
Alien technology, conjunction and ergodicity
-
- Journal:
- International Journal of Astrobiology / Volume 22 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 197-204
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear Markov chains with finite state space: invariant distributions and long-term behaviour
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 30-44
- Print publication:
- March 2023
-
- Article
- Export citation
Chapter 9 - What’s in a Name?
-
- Book:
- Toward a Process Approach in Psychology
- Published online:
- 14 July 2022
- Print publication:
- 28 July 2022, pp 189-214
-
- Chapter
- Export citation
Construction of age-structured branching processes by stochastic equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 May 2022, pp. 670-684
- Print publication:
- September 2022
-
- Article
-
- You have access
- HTML
- Export citation
Ergodicity of Iwasawa continued fractions via markable hyperbolic geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 28 March 2022, pp. 1666-1711
- Print publication:
- May 2023
-
- Article
- Export citation
4 - Overview of Mathematical Tools
- from Part I - Fundamentals
-
- Book:
- Electronic Sensor Design Principles
- Published online:
- 23 December 2021
- Print publication:
- 06 January 2022, pp 189-235
-
- Chapter
- Export citation
Dynamical behavior of alternate base expansions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 22 December 2021, pp. 827-860
- Print publication:
- March 2023
-
- Article
- Export citation
Smoothness of stable holonomies inside center-stable manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3593-3618
- Print publication:
- December 2022
-
- Article
- Export citation
Population dynamics driven by truncated stable processes with Markovian switching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 505-522
- Print publication:
- June 2021
-
- Article
- Export citation