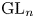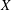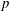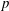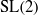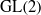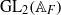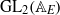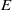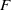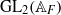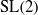Refine search
Actions for selected content:
5 results
Branching laws for classical groups: the non-tempered case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2298-2367
- Print publication:
- November 2020
-
- Article
- Export citation
Product formula for p -adic epsilon factors
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 275-377
- Print publication:
- April 2015
-
- Article
- Export citation
A local-global question in automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 26 April 2013, pp. 959-995
- Print publication:
- June 2013
-
- Article
- Export citation
Facteurs epsilon p-adiques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 439-483
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Calculs de facteurs epsilon de paires sur un corps local, II
-
- Journal:
- Compositio Mathematica / Volume 123 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 89-115
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation