6 results
ON MODEL-THEORETIC CONNECTED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 50-79
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERIZING O-MINIMAL GROUPS IN TAME EXPANSIONS OF O-MINIMAL STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 16 July 2019, pp. 699-724
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
PSEUDOFINITE H-STRUCTURES AND GROUPS DEFINABLE IN SUPERSIMPLE H-STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 02 April 2019, pp. 937-956
- Print publication:
- September 2019
-
- Article
- Export citation
Stability and stable groups in continuous logic
-
- Journal:
- The Journal of Symbolic Logic / Volume 75 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1111-1136
- Print publication:
- September 2010
-
- Article
- Export citation
Definability of groups in ℵ0-stable metric structures
-
- Journal:
- The Journal of Symbolic Logic / Volume 75 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 12 March 2014, pp. 817-840
- Print publication:
- September 2010
-
- Article
- Export citation
O-minimal spectra, infinitesimal subgroups and cohomology
-
- Journal:
- The Journal of Symbolic Logic / Volume 72 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1177-1193
- Print publication:
- December 2007
-
- Article
- Export citation

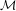
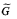 of
of 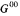 is acyclic in Čech cohomology and Ψ is an isomorphism. Finally we prove the conjecture in some special cases.
is acyclic in Čech cohomology and Ψ is an isomorphism. Finally we prove the conjecture in some special cases.