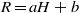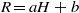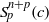Refine search
Actions for selected content:
6 results
An isoperimetric type inequality in De Sitter space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-20
-
- Article
- Export citation
A class of Hessian quotient equations in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 805-821
- Print publication:
- September 2024
-
- Article
- Export citation
Prescribed k-symmetric curvature hypersurfaces in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 26 November 2020, pp. 886-901
- Print publication:
- December 2021
-
- Article
- Export citation
COMPLETE SPACELIKE SUBMANIFOLDS IN DE SITTER SPACES WITH
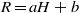 $R= aH+ b$
$R= aH+ b$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 13 February 2013, pp. 386-399
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
BIHARMONIC SUBMANIFOLDS IN NONFLAT LORENTZ 3-SPACE FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 422-432
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Space-like submanifolds with parallel mean curvature in de Sitter spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation