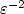Refine search
Actions for selected content:
8 results
An Anisotropic Convection-Diffusion Model Using Tailored Finite Point Method for Image Denoising and Compression
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1357-1374
- Print publication:
- May 2016
-
- Article
- Export citation
Error Analysis for a Non-Monotone FEM for a Singularly Perturbed Problem with Two Small Parameters
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 10 March 2015, pp. 196-206
- Print publication:
- April 2015
-
- Article
- Export citation
Numerical Schemes for Linear and Non-Linear Enhancement of DW-MRI
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 138-168
- Print publication:
- February 2013
-
- Article
- Export citation
Numerical Analysis of a System of Singularly Perturbed Convection-Diffusion Equations Related to Optimal Control
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 4 / Issue 4 / November 2011
- Published online by Cambridge University Press:
- 28 May 2015, pp. 562-575
- Print publication:
- November 2011
-
- Article
- Export citation
Exponential Compact Higher Order Scheme for Nonlinear Steady Convection-Diffusion Equations
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 4 / April 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 897-916
- Print publication:
- April 2011
-
- Article
- Export citation
Homogenization of periodic non self-adjoint problemswith large drift and potential
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 20 July 2007, pp. 735-749
- Print publication:
- October 2007
-
- Article
- Export citation
Solution of degenerate parabolic variational inequalities withconvection
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 15 April 2004, pp. 417-431
- Print publication:
- May 2003
-
- Article
- Export citation
Convergence rate of a finite volume scheme for the linear convection-diffusion equation on locally refined meshes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 34 / Issue 6 / November 2000
- Published online by Cambridge University Press:
- 15 April 2002, pp. 1123-1149
- Print publication:
- November 2000
-
- Article
- Export citation
 (
(