Let G be a simple algebraic group of adjoint type over an algebraically closed field k of bad characteristic. We show that its sheets of conjugacy classes are parametrized by G-conjugacy classes of pairs $(M,{\mathcal O})$ where M is the identity component of the centralizer of a semisimple element in G and ${\mathcal O}$ is a rigid unipotent conjugacy class in M, in analogy with the good characteristic case.

Let $G$ be a primitive permutation group of degree $n$ with nonabelian socle, and let $k(G)$ be the number of conjugacy classes of $G$. We prove that either $k(G)< n/2$ and $k(G)=o(n)$ as $n\rightarrow \infty$, or $G$ belongs to explicit families of examples.

Let $K$ be a subgroup of a finite group $G$. The probability that an element of $G$ commutes with an element of $K$ is denoted by $Pr(K,G)$. Assume that $Pr(K,G)\geq \epsilon$ for some fixed $\epsilon >0$. We show that there is a normal subgroup $T\leq G$ and a subgroup $B\leq K$ such that the indices $[G:T]$ and $[K:B]$ and the order of the commutator subgroup $[T,B]$ are $\epsilon$-bounded. This extends the well-known theorem, due to P. M. Neumann, that covers the case where $K=G$. We deduce a number of corollaries of this result. A typical application is that if $K$ is the generalized Fitting subgroup $F^{*}(G)$ then $G$ has a class-2-nilpotent normal subgroup $R$ such that both the index $[G:R]$ and the order of the commutator subgroup $[R,R]$ are $\epsilon$-bounded. In the same spirit we consider the cases where $K$ is a term of the lower central series of $G$, or a Sylow subgroup, etc.

Let $G$ be a finite group and let $N$ be a normal subgroup of $G$. We determine the structure of $N$ when the diameter of the graph associated to the $G$-conjugacy classes contained in $N$ is as large as possible, that is, equal to three.

We discuss some of the work of Laci Kovács on representation theory and related topics.

We consider finite groups in which, for all primes p, the p-part of the length of any conjugacy class is trivial or fixed. We obtain a full description in the case in which for each prime divisor p of the order of the group there exists a noncentral conjugacy class of p-power size.

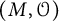
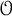
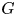
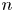
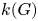
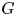
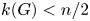
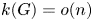
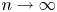
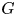
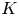
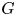
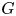
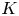
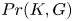
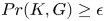
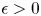
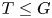
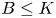
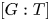
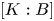
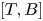
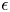
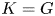
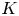
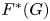
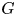
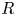
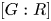
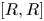
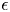
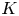
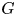
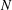
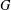
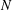
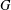
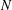
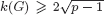Let G be a finite group, let p be a prime divisor of the order of G and let k(G) be the number of conjugacy classes of G. By disregarding at most finitely many non-solvable p-solvable groups G, we have with equality if and only if if 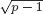is an integer, 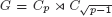and CG(Cp) = Cp. This extends earlier work of Héthelyi, Külshammer, Malle and Keller.

We consider finite p-groups G in which every cyclic subgroup has at most p conjugates. We show that the derived subgroup of such a group has order at most p2. Further, if the stronger condition holds that all subgroups have at most p conjugates then the central factor group has order p4 at most.

An old question of Brauer that asks how fast numbers of conjugacy classes grow is investigated by considering the least number cn of conjugacy classes in a group of order 2n. The numbers cn are computed for n ≤ 14 and a lower bound is given for c15. It is observed that cn grows very slowly except for occasional large jumps corresponding to an increase in coclass of the minimal groups Gn. Restricting to groups that are 2-generated or have coclass at most 3 allows us to extend these computations.

We make several conjectures, and prove some results, pertaining to conjugacy classes of a given size in finite groups, especially in p-groups and 2-groups.