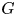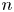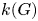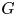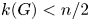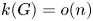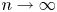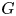1. Introduction
Throughout, $k(G)$![]() denotes the number of conjugacy classes of a finite group $G$
denotes the number of conjugacy classes of a finite group $G$![]() . Maróti [Reference Maróti20] proved that if $G$
. Maróti [Reference Maróti20] proved that if $G$![]() is a primitive permutation group of degree $n$
is a primitive permutation group of degree $n$![]() , then $k(G)\leqslant p(n)$
, then $k(G)\leqslant p(n)$![]() , where $p(n)$
, where $p(n)$![]() denotes the number of partitions of $n$
denotes the number of partitions of $n$![]() . This bound is attained by $S_n$
. This bound is attained by $S_n$![]() in its action on $n$
in its action on $n$![]() points. Moreover, he proved that if the socle of $G$
points. Moreover, he proved that if the socle of $G$![]() is not a direct product of alternating groups, then $k(G)\leqslant n^{6}$
is not a direct product of alternating groups, then $k(G)\leqslant n^{6}$![]() .
.
In this paper, we want to improve this bound under the assumption that $G$![]() has nonabelian socle. In § 1.2, we will give more context and review more results in this area.
has nonabelian socle. In § 1.2, we will give more context and review more results in this area.
There are two special types of primitive groups which we wish to single out.
(A) Let $G$
 be the symmetric group $S_d$
be the symmetric group $S_d$ or the alternating group $A_d$
or the alternating group $A_d$ on $d\geqslant 5$
on $d\geqslant 5$ letters. For every $1\leqslant k< d/2$
letters. For every $1\leqslant k< d/2$ , $G$
, $G$ acts primitively on the set of $k$
acts primitively on the set of $k$ -subsets of $\{1, \ldots, d\}$
-subsets of $\{1, \ldots, d\}$ . These are in number $\binom {d}{k}$
. These are in number $\binom {d}{k}$ .
.(B) Let $G$
 be an almost simple group with socle $\mathrm {PSL}_d(q)$
be an almost simple group with socle $\mathrm {PSL}_d(q)$ , and assume that $G\leqslant \mathrm {P\Gamma L}_d(q)$
, and assume that $G\leqslant \mathrm {P\Gamma L}_d(q)$ . Then $G$
. Then $G$ acts primitively on the set of $1$
acts primitively on the set of $1$ -subspaces of $\mathbf {F}_q^{d}$
-subspaces of $\mathbf {F}_q^{d}$ . These are in number $(q^{d}-1)/(q-1)$
. These are in number $(q^{d}-1)/(q-1)$ .
.
Our main result says that, if $G$![]() is a primitive group with nonabelian socle, then either $G$
is a primitive group with nonabelian socle, then either $G$![]() has very few conjugacy classes, or else the action of $G$
has very few conjugacy classes, or else the action of $G$![]() is ‘related’ to (A) or (B) or to a further finitely many almost simple primitive permutation groups. The precise statement is as follows.
is ‘related’ to (A) or (B) or to a further finitely many almost simple primitive permutation groups. The precise statement is as follows.
Theorem 1.1 Let $G$![]() be a primitive permutation group of degree $n$
be a primitive permutation group of degree $n$![]() with nonabelian socle, so $\mathrm {Soc}(G)\cong S^{r}$
with nonabelian socle, so $\mathrm {Soc}(G)\cong S^{r}$![]() , with $S$
, with $S$![]() nonabelian simple and $r\geqslant 1$
nonabelian simple and $r\geqslant 1$![]() . Then one of the following holds.
. Then one of the following holds.
(1) $k(G)< n/2$
 , and $k(G)=O(n^{\delta })$
, and $k(G)=O(n^{\delta })$ for some absolute $\delta <1$
for some absolute $\delta <1$ .
.(2) $G\leqslant A\wr S_r$
 , $A$
, $A$ is an almost simple primitive permutation group of degree $m$
is an almost simple primitive permutation group of degree $m$ with socle $S$
with socle $S$ , $G$
, $G$ acts in product action on $n=m^{r}$
acts in product action on $n=m^{r}$ points, and one of the following holds:
points, and one of the following holds:
(i) The action of $A$
 on $m$
on $m$ points is equivalent to an action in table 1, and $k(G)< n^{1.31}$
points is equivalent to an action in table 1, and $k(G)< n^{1.31}$ .
.(ii) The action of $A$
 on $m$
on $m$ points is isomorphic to an action described in (A) or (B). In the (B)-case, $k(G)< n^{1.9}$
points is isomorphic to an action described in (A) or (B). In the (B)-case, $k(G)< n^{1.9}$ .
.
Table 1. Almost simple primitive permutation groups $G$![]() of degree $n$
of degree $n$![]() (up to equivalence) for which $k(G)\geqslant \frac n2$
(up to equivalence) for which $k(G)\geqslant \frac n2$![]() , and for which the action is not isomorphic to an action in (A) or (B)
, and for which the action is not isomorphic to an action in (A) or (B)

On the way, we remark that theorem 1.1 is a key ingredient of the paper [Reference Garzoni and Gill9], where we study a problem of invariable generation of symmetric groups.
We will first prove theorem 1.1 in case $G$![]() is almost simple, and then deduce the general case. For convenience, we state separately the almost simple case (where we also give an explicit estimate for $\delta$
is almost simple, and then deduce the general case. For convenience, we state separately the almost simple case (where we also give an explicit estimate for $\delta$![]() ).
).
Theorem 1.2 Let $G$![]() be an almost simple primitive permutation group of degree $n$
be an almost simple primitive permutation group of degree $n$![]() . Then one of the following holds.
. Then one of the following holds.
(1) $k(G)< n/2$
 , and $k(G)=O(n^{3/4})$
, and $k(G)=O(n^{3/4})$ .
.(2) Either the action of $G$
 is equivalent to an action in table 1, or the action of $G$
is equivalent to an action in table 1, or the action of $G$ is isomorphic to an action described in (A) or (B). In the (B)-case, $k(G)< 100n$
is isomorphic to an action described in (A) or (B). In the (B)-case, $k(G)< 100n$ .
.
In item (1), the exponent $3/4$![]() is sharp, although in most cases $k(G)=o(n^{3/4})$
is sharp, although in most cases $k(G)=o(n^{3/4})$![]() as $n\rightarrow \infty$
as $n\rightarrow \infty$![]() ; see remark 2.14 for a precise statement.
; see remark 2.14 for a precise statement.
In the proof of theorem 1.2, an essential ingredient is the work of Fulman–Guralnick [Reference Fulman and Guralnick6], which gives upper bounds for the number of conjugacy classes of almost simple groups of Lie type.
We immediately make some clarifications regarding the statement of theorem 1.1.
Remark 1.3
(i) We are not asserting that every case appearing in theorem 1.1(2) does not satisfy item (1). For instance, assume that $m=n$
 , and consider $G=S_d$
, and consider $G=S_d$ acting on $n=\binom {d}{k}$
acting on $n=\binom {d}{k}$ points as in (A), and assume that $cd\leqslant k\leqslant \frac {d}{2}$
points as in (A), and assume that $cd\leqslant k\leqslant \frac {d}{2}$ for some fixed constant $c$
for some fixed constant $c$ . Then it is well known that $n=\binom {d}{k}$
. Then it is well known that $n=\binom {d}{k}$ is exponential in $d$
is exponential in $d$ , while the number of conjugacy classes of $G=S_d$
, while the number of conjugacy classes of $G=S_d$ is of the form $O(1)^{\sqrt d}$
is of the form $O(1)^{\sqrt d}$ . In particular $k(G)=n^{o(1)}$
. In particular $k(G)=n^{o(1)}$ as $d\rightarrow \infty$
as $d\rightarrow \infty$ .
.(ii) In theorem 1.1(2)(ii), we can be more precise about the adjective isomorphic, as follows. If $A$
 is $A_d$
is $A_d$ or $S_d$
or $S_d$ , then either the action of $A$
, then either the action of $A$ is equivalent to the action on $k$
is equivalent to the action on $k$ -subsets; or else $(d,m)=(6,6)$
-subsets; or else $(d,m)=(6,6)$ or $(6,15)$
or $(6,15)$ . Moreover, if $A$
. Moreover, if $A$ is almost simple with socle $\mathrm {PSL}_d(q)$
is almost simple with socle $\mathrm {PSL}_d(q)$ and $A\leqslant \mathrm {P\Gamma L}_d(q)$
and $A\leqslant \mathrm {P\Gamma L}_d(q)$ , then the action of $A$
, then the action of $A$ is equivalent to the action on the $1$
is equivalent to the action on the $1$ -subspaces or $(d-1)$
-subspaces or $(d-1)$ -subspaces of $\mathbf {F}_q^{d}$
-subspaces of $\mathbf {F}_q^{d}$ . For this, see lemmas 2.8 and 2.12.
. For this, see lemmas 2.8 and 2.12.(iii) Whenever $G$
 is almost simple with socle isomorphic to both $A_d$
is almost simple with socle isomorphic to both $A_d$ and $\mathrm {PSL}_f(q)$
and $\mathrm {PSL}_f(q)$ , we have excluded from table 1 both the groups in (A) and (B). For instance, $G=S_6$
, we have excluded from table 1 both the groups in (A) and (B). For instance, $G=S_6$ has $11$
has $11$ conjugacy classes, and contains a subgroup $S_3\wr S_2$
conjugacy classes, and contains a subgroup $S_3\wr S_2$ of index $10$
of index $10$ acting transitively on $6$
acting transitively on $6$ points; but this does not appear in table 1 in view of the isomorphism $S_6\cong \text P\Sigma \text L_2(9)$
points; but this does not appear in table 1 in view of the isomorphism $S_6\cong \text P\Sigma \text L_2(9)$ . The same reasoning applies to the isomorphisms $\mathrm {SL}_2(4)\cong \mathrm {PSL}_2(5)\cong A_5$
. The same reasoning applies to the isomorphisms $\mathrm {SL}_2(4)\cong \mathrm {PSL}_2(5)\cong A_5$ , $\mathrm {PSL}_2(7)\cong \mathrm {SL}_3(2)$
, $\mathrm {PSL}_2(7)\cong \mathrm {SL}_3(2)$ and $\mathrm {SL}_4(2)\cong A_8$
and $\mathrm {SL}_4(2)\cong A_8$ .
.
1.1 When is $k(G)=o(n)$ ?
?
Theorem 1.1 implies in particular that, if the socle of $G$![]() is nonabelian, then either $k(G)=o(n)$
is nonabelian, then either $k(G)=o(n)$![]() , or $G$
, or $G$![]() is ‘known’. Can we prove that $k(G)=o(n)$
is ‘known’. Can we prove that $k(G)=o(n)$![]() in further cases?
in further cases?
We are particularly interested in the cases contemplated in theorem 1.1(2)(i), for which we show $k(G)< n^{1.31}$![]() . We first note that there are examples in which $k(G)> n^{1.08}$
. We first note that there are examples in which $k(G)> n^{1.08}$![]() for arbitrarily large $n$
for arbitrarily large $n$![]() , in contrast to item (1); see lemma 4.1.
, in contrast to item (1); see lemma 4.1.
Still, it would be interesting to understand precisely when this happens (since there are only finitely many almost simple groups to handle).
Question 1 Let $A$![]() be an almost simple primitive group on $m$
be an almost simple primitive group on $m$![]() points appearing in table 1. Determine whether every primitive subgroup $G$
points appearing in table 1. Determine whether every primitive subgroup $G$![]() of $A\wr S_r$
of $A\wr S_r$![]() on $n=m^{r}$
on $n=m^{r}$![]() points is such that $k(G)=o(m^{r})$
points is such that $k(G)=o(m^{r})$![]() as $r\rightarrow \infty$
as $r\rightarrow \infty$![]() .
.
This should be related to estimating the number of conjugacy classes in wreath products, and we refer to § 4 for comments in this direction. See in particular conjecture 4.2, which would provide an answer to question 1.
1.2 Context
There are many results in the literature which give upper bounds to the number of conjugacy classes of a finite groups in terms of various parameters. We recall some of these, focusing on permutation groups.
Kovács–Robinson [Reference Kovács and Robinson16] proved that every permutation group of degree $n$![]() has at most $5^{n-1}$
has at most $5^{n-1}$![]() conjugacy classes. This estimate was subsequently improved by Liebeck–Pyber, Maróti, and Garonzi–Maróti, as follows:
conjugacy classes. This estimate was subsequently improved by Liebeck–Pyber, Maróti, and Garonzi–Maróti, as follows:

We should mention that, in [Reference Kovács and Robinson16, Reference Liebeck and Pyber17], various other upper bounds to $k(G)$![]() are proved, where $G$
are proved, where $G$![]() is not necessarily a permutation group.
is not necessarily a permutation group.
There are easy examples showing that these estimates are somewhat close to best possible, even for transitive groups. Indeed, the subgroup $S_4^{n/4}\leqslant S_n$![]() has $5^{n/4}$
has $5^{n/4}$![]() conjugacy classes; and the transitive subgroup $G=S_4\wr C_{n/4}\leqslant S_n$
conjugacy classes; and the transitive subgroup $G=S_4\wr C_{n/4}\leqslant S_n$![]() has $5^{n/4-o(n)}$
has $5^{n/4-o(n)}$![]() conjugacy classes (more precisely, $k(G)$
conjugacy classes (more precisely, $k(G)$![]() is asymptotic to $4\cdot 5^{n/4}/n$
is asymptotic to $4\cdot 5^{n/4}/n$![]() ; see lemma 4.3).
; see lemma 4.3).
For primitive groups, the situation is very different. Let $G$![]() be a primitive permutation group of degree $n$
be a primitive permutation group of degree $n$![]() . Liebeck–Pyber [Reference Liebeck and Pyber17, corollary 2.15] proved the following:
. Liebeck–Pyber [Reference Liebeck and Pyber17, corollary 2.15] proved the following:
(i) $k(G)\leqslant p(n)$
 if $n$
if $n$ is sufficiently large;
is sufficiently large;(ii) $k(G)\leqslant n^{11}$
 if the socle of $G$
if the socle of $G$ is not a direct product of alternating groups.
is not a direct product of alternating groups.
(Recall that $p(n)=O(1)^{\sqrt n}$![]() , and in fact the asymptotic behaviour of $p(n)$
, and in fact the asymptotic behaviour of $p(n)$![]() is known by famous work of Hardy–Ramanujan.) Maróti [Reference Maróti20] improved these results. He showed that item (i) holds for every positive integer $n$
is known by famous work of Hardy–Ramanujan.) Maróti [Reference Maróti20] improved these results. He showed that item (i) holds for every positive integer $n$![]() and, moreover, the bound $k(N)\leqslant p(n)$
and, moreover, the bound $k(N)\leqslant p(n)$![]() holds for every normal subgroup $N$
holds for every normal subgroup $N$![]() of $G$
of $G$![]() . He also showed that, in item (ii), one can replace $n^{11}$
. He also showed that, in item (ii), one can replace $n^{11}$![]() by $n^{6}$
by $n^{6}$![]() .
.
Theorem 1.1 can be regarded as an improvement of these statements, for the case where the socle of $G$![]() is nonabelian.
is nonabelian.
1.3 Abelian socle
In this paper we do not address the case in which the socle of $G$![]() is abelian. In this case, we still have the bound $k(G)\leqslant n^{6}$
is abelian. In this case, we still have the bound $k(G)\leqslant n^{6}$![]() from [Reference Maróti20].
from [Reference Maróti20].
There is a deep problem, known as the non-coprime $k(GV)$![]() -problem, which was addressed by Guralnick–Tiep [Reference Guralnick and Tiep13] and which asks (in particular) for a characterization of the affine primitive permutation groups of degree $n$
-problem, which was addressed by Guralnick–Tiep [Reference Guralnick and Tiep13] and which asks (in particular) for a characterization of the affine primitive permutation groups of degree $n$![]() for which $k(G)>n$
for which $k(G)>n$![]() . A resolution of this problem, if combined with the main result of this paper, would give a characterization of all primitive permutation groups of degree $n$
. A resolution of this problem, if combined with the main result of this paper, would give a characterization of all primitive permutation groups of degree $n$![]() for which $k(G)>n$
for which $k(G)>n$![]() . We refer to Guralnick–Tiep [Reference Guralnick and Tiep13], Guralnick–Maróti [Reference Guralnick and Maróti10] and the references therein for results in this direction, partly motivated by Brauer's celebrated $k(B)$
. We refer to Guralnick–Tiep [Reference Guralnick and Tiep13], Guralnick–Maróti [Reference Guralnick and Maróti10] and the references therein for results in this direction, partly motivated by Brauer's celebrated $k(B)$![]() -conjecture.
-conjecture.
The organization of the paper is as follows. In § 2 we prove theorem 1.2, in § 3 we prove theorem 1.1, and in § 4 we discuss question 1 and make further comments.
2. Almost simple groups
In this section we prove theorem 1.2. Regarding item (1), we prove the inequality $k(G)< n/2$![]() in §2.2–2.4, and then we prove the asymptotic inequality $k(G)=O(n^{3/4})$
in §2.2–2.4, and then we prove the asymptotic inequality $k(G)=O(n^{3/4})$![]() in § 2.5.
in § 2.5.
2.1 Some preliminary lemmas
We begin with a lemma from [Reference Gallagher7]. We will often apply this lemma with no mention.
Lemma 2.1 If $G$![]() is a finite group and $H$
is a finite group and $H$![]() is a subgroup of $G$
is a subgroup of $G$![]() , then
, then
If moreover $H$![]() is normal in $G$
is normal in $G$![]() , then
, then
In one occasion, we will need the following variant (see [Reference Kovács and Robinson16, p. 447]).
Lemma 2.2 Let $G$![]() be a finite group and let $N$
be a finite group and let $N$![]() be a normal subgroup of $G$
be a normal subgroup of $G$![]() . Then
. Then
We are now ready to begin the proof of theorem 1.2.
2.2 Sporadic groups
Lemma 2.3 Let $G$![]() be almost simple with socle $S$
be almost simple with socle $S$![]() , a sporadic simple group. Let $M$
, a sporadic simple group. Let $M$![]() be a core-free maximal subgroup of $G$
be a core-free maximal subgroup of $G$![]() , and write $n=|G:M|$
, and write $n=|G:M|$![]() . If $k(G)\geqslant \frac {n}{2}$
. If $k(G)\geqslant \frac {n}{2}$![]() , then $G$
, then $G$![]() and $n$
and $n$![]() are listed in table 2.
are listed in table 2.
Table 2. Faithful primitive permutation representations of degree $n$![]() for sporadic almost simple groups $G$
for sporadic almost simple groups $G$![]() such that $k(G)\geqslant \frac {n}2$
such that $k(G)\geqslant \frac {n}2$![]()

Note that repeated values of $n$![]() in table 2 signify the existence of more than one action, up to equivalence, of the given degree. The same convention applies to later tables pertaining to the alternating groups and the groups of Lie type.
in table 2 signify the existence of more than one action, up to equivalence, of the given degree. The same convention applies to later tables pertaining to the alternating groups and the groups of Lie type.
Proof. We go through the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson3].
2.3 Alternating groups
We recall some results that we will use. The first is an inequality of Pribitkin [Reference Pribitkin22], as follows.
Lemma 2.4 Let $p(d)$![]() be the number of partitions of the integer $d$
be the number of partitions of the integer $d$![]() . Then
. Then
We will need the following pair of inequalities which are an easy consequence of work of Robbins on the Stirling approximations [Reference Robbins24].
Lemma 2.5 Let $d\geqslant 2$![]() be an integer. Then
be an integer. Then
We will also need the following result of Praeger and Saxl [Reference Praeger and Saxl23].
Lemma 2.6 Let $G\leqslant S_d$![]() and suppose that $G$
and suppose that $G$![]() is primitive and does not contain $A_d$
is primitive and does not contain $A_d$![]() . Then $|G|<4^{d}$
. Then $|G|<4^{d}$![]() .
.
Finally, we will need an elementary lemma. For a proof, see for instance [Reference Guralnick and Tiep13, lemma 6.2].
Lemma 2.7 For every positive integer $d$![]() , $k(A_d)\leqslant k(S_d)$
, $k(A_d)\leqslant k(S_d)$![]() .
.
Now we can prove the main result of this subsection.
Lemma 2.8 Let $G$![]() be almost simple with socle $S\cong A_d$
be almost simple with socle $S\cong A_d$![]() . Let $M$
. Let $M$![]() be a core-free maximal subgroup of $G$
be a core-free maximal subgroup of $G$![]() , and write $n=|G:M|$
, and write $n=|G:M|$![]() . If $k(G)\geqslant \frac {n}{2}$
. If $k(G)\geqslant \frac {n}{2}$![]() , then one of the following holds.
, then one of the following holds.
(1) $G$
 and $n$
and $n$ are listed in table 3.
are listed in table 3.(2) $M$
 is intransitive in its action on $d$
is intransitive in its action on $d$ points, thus $n=\binom {d}{k}$
points, thus $n=\binom {d}{k}$ for some integer $k$
for some integer $k$ such that $1\leqslant k< \frac {1}{2}d$
such that $1\leqslant k< \frac {1}{2}d$ .
.(3) $(d,n)=(6,6)$
 or $(6,15)$
or $(6,15)$ , and the action of $G$
, and the action of $G$ on the cosets of $M$
on the cosets of $M$ is isomorphic, but not equivalent, to the action on the coset of a maximal intransitive subgroup.
is isomorphic, but not equivalent, to the action on the coset of a maximal intransitive subgroup.
Table 3. Faithful primitive permutation representations of degree $n$![]() for almost simple groups $G$
for almost simple groups $G$![]() with socle $A_d$
with socle $A_d$![]() such that $k(G)\geqslant \frac n2$
such that $k(G)\geqslant \frac n2$![]() , and the action is not isomorphic to an action in (A)
, and the action is not isomorphic to an action in (A)

In item (3), if $(d,n)=(6,6)$![]() we have $G=A_6$
we have $G=A_6$![]() or $S_6$
or $S_6$![]() , and $M=S_5\cap G$
, and $M=S_5\cap G$![]() , where $S_5$
, where $S_5$![]() is a subgroup of $S_6$
is a subgroup of $S_6$![]() acting primitively on $6$
acting primitively on $6$![]() points. If $(d,n)=(6,15)$
points. If $(d,n)=(6,15)$![]() , again $G=A_6$
, again $G=A_6$![]() or $S_6$
or $S_6$![]() , and $M=(S_2\wr S_3)\cap G$
, and $M=(S_2\wr S_3)\cap G$![]() , where $S_2\wr S_3$
, where $S_2\wr S_3$![]() acts transitively (and imprimitively) on $6$
acts transitively (and imprimitively) on $6$![]() points. (Note that in the latter case, if $G=A_6$
points. (Note that in the latter case, if $G=A_6$![]() then $k(G)< n/2$
then $k(G)< n/2$![]() .)
.)
Proof. For $d\leqslant 8$![]() , we use the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson3] together with GAP [8] to obtain the given list. For $9\leqslant d \leqslant 20$
, we use the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson3] together with GAP [8] to obtain the given list. For $9\leqslant d \leqslant 20$![]() we use GAP to check that no examples occur. Assume, then, that $d>20$
we use GAP to check that no examples occur. Assume, then, that $d>20$![]() .
.
Let us suppose, first, that $M$![]() is primitive in its action on $d$
is primitive in its action on $d$![]() points. Then lemmas 2.4–2.7 imply that it is sufficient to prove the following
points. Then lemmas 2.4–2.7 imply that it is sufficient to prove the following
If we assume that the other inequality holds, we get

Since $d>20$![]() , the result follows.
, the result follows.
Let us suppose, next, that $M$![]() is imprimitive in its action on $d$
is imprimitive in its action on $d$![]() points. Then
points. Then
where $d=k\ell$![]() and $k, \ell \geqslant 2$
and $k, \ell \geqslant 2$![]() . Now lemma 2.5 implies that
. Now lemma 2.5 implies that

which implies that

(In this proof, all logarithms are base two.) If we fix $d$![]() and set $f(\ell )$
and set $f(\ell )$![]() to be the function on the left-hand side of the final inequality, with $\ell \in (0,d)$
to be the function on the left-hand side of the final inequality, with $\ell \in (0,d)$![]() , then one computes that $f'(\ell )$
, then one computes that $f'(\ell )$![]() is a decreasing function. In particular, $f(\ell )$
is a decreasing function. In particular, $f(\ell )$![]() takes its minimum value in the range $\ell \in (0,d)$
takes its minimum value in the range $\ell \in (0,d)$![]() either when $\ell$
either when $\ell$![]() is as large as possible or as small as possible.
is as large as possible or as small as possible.
If $\ell$![]() is as small as possible, then $\ell =2$
is as small as possible, then $\ell =2$![]() and we obtain that
and we obtain that
If $\ell$![]() is as large as possible, then $\ell =\frac {d}{2}$
is as large as possible, then $\ell =\frac {d}{2}$![]() and we obtain that
and we obtain that
Now it is easy to check that, for $d\geqslant 4$![]() ,
,
and we conclude that
On the other hand, if $k(G)\geqslant \frac {n}{2}$![]() , then lemmas 2.4 and 2.7 imply that
, then lemmas 2.4 and 2.7 imply that
Taking logs and using (2.1), we get
which, since $d>20$![]() , is false. This concludes the proof.
, is false. This concludes the proof.
2.4 Groups of Lie type
For groups of Lie type, we will use results of Fulman and Guralnick giving bounds on the number of conjugacy classes.
Theorem 2.9 [Reference Fulman and Guralnick6, theorem 1.1]
Let $G$![]() be a connected simple algebraic group of rank $r$
be a connected simple algebraic group of rank $r$![]() over a field of positive characteristic. Let $F$
over a field of positive characteristic. Let $F$![]() be a Steinberg endomorphism of $G$
be a Steinberg endomorphism of $G$![]() with $G^{F}$
with $G^{F}$![]() a finite group of Lie type over the field $\mathbf {F}_q$
a finite group of Lie type over the field $\mathbf {F}_q$![]() . Then
. Then
Theorem 2.10 [Reference Fulman and Guralnick6, corollary 1.2]
Let $G$![]() be an almost simple group with socle $S$
be an almost simple group with socle $S$![]() , a simple group of Lie type of untwisted rank $r$
, a simple group of Lie type of untwisted rank $r$![]() defined over $\mathbf {F}_q$
defined over $\mathbf {F}_q$![]() . Then $k(G)\leqslant 100q^{r}$
. Then $k(G)\leqslant 100q^{r}$![]() .
.
We also introduce the following notation. For a finite group $G$![]() , let $P(G)$
, let $P(G)$![]() be the minimal degree of a faithful permutation representation of $G$
be the minimal degree of a faithful permutation representation of $G$![]() . If $G$
. If $G$![]() is almost simple with socle $S$
is almost simple with socle $S$![]() , then $P(G)$
, then $P(G)$![]() coincides with the minimal degree of a faithful transitive permutation representation of $G$
coincides with the minimal degree of a faithful transitive permutation representation of $G$![]() , and moreover $P(S)\leqslant P(G)$
, and moreover $P(S)\leqslant P(G)$![]() . The values of $P(G)$
. The values of $P(G)$![]() for $G$
for $G$![]() a finite simple group are known; they are listed for instance in [Reference Guest, Morris, Praeger and Spiga12, table 4].
a finite simple group are known; they are listed for instance in [Reference Guest, Morris, Praeger and Spiga12, table 4].
Now we deal with exceptional groups.
Lemma 2.11 Let $G$![]() be almost simple with socle $S$
be almost simple with socle $S$![]() , a simple exceptional group of Lie type. Then $k(G)< \frac {1}{2}|G:M|$
, a simple exceptional group of Lie type. Then $k(G)< \frac {1}{2}|G:M|$![]() for all core-free maximal subgroups $M$
for all core-free maximal subgroups $M$![]() of $G$
of $G$![]() .
.
Proof. We prove the stronger inequality $k(G)< P(S)/2$![]() . We use the values for $P(S)$
. We use the values for $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12], as well as the fact that $k(G)\leqslant 100q^{r}$
given in [Reference Guest, Morris, Praeger and Spiga12], as well as the fact that $k(G)\leqslant 100q^{r}$![]() (from theorem 2.10).
(from theorem 2.10).
If $S$![]() is not a Suzuki group, then the value of $P(S)$
is not a Suzuki group, then the value of $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12] is sufficient to prove that $k(G)< P(S)/2$
given in [Reference Guest, Morris, Praeger and Spiga12] is sufficient to prove that $k(G)< P(S)/2$![]() , except for the groups with socle $G_2(3)$
, except for the groups with socle $G_2(3)$![]() , $G_2(4)$
, $G_2(4)$![]() , $G_2(5)$
, $G_2(5)$![]() , ${{}^{3}\!D_4}(2)$
, ${{}^{3}\!D_4}(2)$![]() , $^{2}\!F_4(2)'$
, $^{2}\!F_4(2)'$![]() and ${{}^{2}\!G_2}(3^{3})$
and ${{}^{2}\!G_2}(3^{3})$![]() . In these cases, we can verify $k(G)< P(S)/2$
. In these cases, we can verify $k(G)< P(S)/2$![]() using the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson3].
using the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson3].
If $S$![]() is a Suzuki group, then [Reference Suzuki25] tells us that $k(S)=q+3$
is a Suzuki group, then [Reference Suzuki25] tells us that $k(S)=q+3$![]() , and lemma 2.1 implies that $k(G)$
, and lemma 2.1 implies that $k(G)$![]() is at most $(q+3)f$
is at most $(q+3)f$![]() , where $q=2^{f}$
, where $q=2^{f}$![]() . On the other hand, $P(S)=q^{2}+1$
. On the other hand, $P(S)=q^{2}+1$![]() by [Reference Guest, Morris, Praeger and Spiga12]. Then $(q+3)f \geqslant \frac 12 (q^{2}+1)$
by [Reference Guest, Morris, Praeger and Spiga12]. Then $(q+3)f \geqslant \frac 12 (q^{2}+1)$![]() if and only if $q=8$
if and only if $q=8$![]() (recall that $f$
(recall that $f$![]() is odd and $f\geqslant 3$
is odd and $f\geqslant 3$![]() ). But if $q=8$
). But if $q=8$![]() , [Reference Conway, Curtis, Norton, Parker and Wilson3] tells us that $S.3$
, [Reference Conway, Curtis, Norton, Parker and Wilson3] tells us that $S.3$![]() has 17 conjugacy classes and in this case, too, we have $k(G)< P(S)/2$
has 17 conjugacy classes and in this case, too, we have $k(G)< P(S)/2$![]() .
.
Next we deal with the case in which $G$![]() has socle $\mathrm {PSL}_d(q)$
has socle $\mathrm {PSL}_d(q)$![]() .
.
Lemma 2.12 Let $G$![]() be almost simple with socle $S\cong \mathrm {PSL}_d(q)$
be almost simple with socle $S\cong \mathrm {PSL}_d(q)$![]() . Let $M$
. Let $M$![]() be a core-free maximal subgroup of $G$
be a core-free maximal subgroup of $G$![]() , and write $n=|G:M|$
, and write $n=|G:M|$![]() . If $k(G)\geqslant \frac {n}{2}$
. If $k(G)\geqslant \frac {n}{2}$![]() , then one of the following holds.
, then one of the following holds.
(1) $G$
 and $n$
and $n$ are listed in table 4.
are listed in table 4.(2) $G\leqslant \mathrm {P\Gamma L}_d(q)$
 and $M$
and $M$ stabilizes a $1$
stabilizes a $1$ -dimensional or a $(d-1)$
-dimensional or a $(d-1)$ -dimensional subspace of $\mathbf {F}_q^{d}$
-dimensional subspace of $\mathbf {F}_q^{d}$ , thus $n=\frac {q^{d}-1}{q-1}$
, thus $n=\frac {q^{d}-1}{q-1}$ .
.
Table 4. Faithful primitive permutation representations of degree $n$![]() for almost simple groups $G$
for almost simple groups $G$![]() with socle $\mathrm {PSL}_d(q)$
with socle $\mathrm {PSL}_d(q)$![]() such that $k(G)\geqslant \frac n2$
such that $k(G)\geqslant \frac n2$![]() , and the action is not isomorphic to an action in (B) (see the remark after the statement of lemma 2.12)
, and the action is not isomorphic to an action in (B) (see the remark after the statement of lemma 2.12)

Note that, in table 4, in order to ensure that the lemma is true, $n=6$![]() appears for $G=\mathrm {SL}_2(4)$
appears for $G=\mathrm {SL}_2(4)$![]() , but not for $G=\mathrm {PSL}_2(5)$
, but not for $G=\mathrm {PSL}_2(5)$![]() (even though $\mathrm {SL}_2(4)\cong \mathrm {PSL}_2(5)$
(even though $\mathrm {SL}_2(4)\cong \mathrm {PSL}_2(5)$![]() ). Similarly, $n=5$
). Similarly, $n=5$![]() appears for $\mathrm {PSL}_2(5)$
appears for $\mathrm {PSL}_2(5)$![]() , but not for $\mathrm {SL}_2(4)$
, but not for $\mathrm {SL}_2(4)$![]() . Similar considerations apply for the isomorphic groups $\mathrm {PSL}_2(7)$
. Similar considerations apply for the isomorphic groups $\mathrm {PSL}_2(7)$![]() and $\mathrm {SL}_3(2)$
and $\mathrm {SL}_3(2)$![]() .
.
Proof. In this proof we use [Reference Kantor14]. The main theorem of this paper, together with theorem 2.10, implies that, if $k(G)\geqslant n/2$![]() , then either $d\leqslant 4$
, then either $d\leqslant 4$![]() , or
, or
or $H:=M\cap \mathrm {P\Gamma L}_d(q)$![]() is reducible, or $H$
is reducible, or $H$![]() normalizes $\mathrm {PSp}_d(q)$
normalizes $\mathrm {PSp}_d(q)$![]() .
.
Assume first that $d\geqslant 5$![]() . This rules out the case in which $H$
. This rules out the case in which $H$![]() normalizes $\mathrm {PSp}_d(q)$
normalizes $\mathrm {PSp}_d(q)$![]() . Let us now consider the case where $H$
. Let us now consider the case where $H$![]() is reducible, stabilizing a subspace of dimension $m$
is reducible, stabilizing a subspace of dimension $m$![]() .
.
Assume first that $2\leqslant m \leqslant d-2$![]() . Then $n=|G:M|>q^{m(d-m)}\geqslant q^{2d-4}$
. Then $n=|G:M|>q^{m(d-m)}\geqslant q^{2d-4}$![]() . If $k(G)\geqslant \frac n2$
. If $k(G)\geqslant \frac n2$![]() then, using theorem 2.10, we deduce that $q^{d-3}<200$
then, using theorem 2.10, we deduce that $q^{d-3}<200$![]() . We want to whittle down the possibilities, as follows. [Reference Fulman and Guralnick6, proposition 3.6] states that $k(\mathrm {PSL}_d(q))\leqslant 2.5q^{d-1}$
. We want to whittle down the possibilities, as follows. [Reference Fulman and Guralnick6, proposition 3.6] states that $k(\mathrm {PSL}_d(q))\leqslant 2.5q^{d-1}$![]() . This, together with the knowledge of $|\mathrm {Out}(S)|$
. This, together with the knowledge of $|\mathrm {Out}(S)|$![]() and lemma 2.1, reduces easily to the cases $(d,q)=(5,2), (5,3), (5,4), (6,2)$
and lemma 2.1, reduces easily to the cases $(d,q)=(5,2), (5,3), (5,4), (6,2)$![]() . The same argument and [Reference Kantor14] rule out the cases $(d,q)=(5,8),(7,2)$
. The same argument and [Reference Kantor14] rule out the cases $(d,q)=(5,8),(7,2)$![]() in (2.2). We can deal with the remaining cases with GAP [8].
in (2.2). We can deal with the remaining cases with GAP [8].
Assume now that $m\in \{1, d-1\}$![]() . The case in which $G\leqslant \mathrm {P\Gamma L}_d(q)$
. The case in which $G\leqslant \mathrm {P\Gamma L}_d(q)$![]() appears in item (2) of the statement. If $G\nleq \mathrm {P\Gamma L}_d(q)$
appears in item (2) of the statement. If $G\nleq \mathrm {P\Gamma L}_d(q)$![]() , then $M$
, then $M$![]() is a novelty and $|G:M|\geqslant q^{2d-3}$
is a novelty and $|G:M|\geqslant q^{2d-3}$![]() , and the GAP calculation from the previous paragraph rules out all possibilities.
, and the GAP calculation from the previous paragraph rules out all possibilities.
Let us turn, then, to study what happens when $d\in \{2,3,4\}$![]() . We make use of the counts given in [Reference Macdonald19].
. We make use of the counts given in [Reference Macdonald19].
When $d=2$![]() , [Reference Macdonald19] implies that
, [Reference Macdonald19] implies that
We use this in combination with the explicit list of maximal subgroups in $\mathrm {PSL}_2(q)$![]() to conclude that either
to conclude that either
(1) $q\leqslant 11$
 ; or
; or(2) $q=16$
 and $M$
and $M$ is the normalizer of a torus, or a subfield subgroup such that $M\cap S\cong \mathrm {PGL}_2(\sqrt {q})$
is the normalizer of a torus, or a subfield subgroup such that $M\cap S\cong \mathrm {PGL}_2(\sqrt {q})$ ; or
; or(3) $q\in \{ 25, 49, 81, 64, 256\}$
 and $M$
and $M$ is a subfield subgroup such that $M\cap S\cong \mathrm {PGL}_2(\sqrt {q})$
is a subfield subgroup such that $M\cap S\cong \mathrm {PGL}_2(\sqrt {q})$ .
.
Using [8] we get the possibilities in table 4.
Next assume that $d=3$![]() . If $q$
. If $q$![]() is odd, then using [Reference Macdonald19] we see that $k(\mathrm {PSL}_3(q))\leqslant q^{2}+q$
is odd, then using [Reference Macdonald19] we see that $k(\mathrm {PSL}_3(q))\leqslant q^{2}+q$![]() , and this, along with [Reference Kantor14], allows us to conclude that $q\leqslant 9$
, and this, along with [Reference Kantor14], allows us to conclude that $q\leqslant 9$![]() . These possibilities can all be excluded using [Reference Conway, Curtis, Norton, Parker and Wilson3]. If $q$
. These possibilities can all be excluded using [Reference Conway, Curtis, Norton, Parker and Wilson3]. If $q$![]() is even, then [Reference Macdonald19] implies that $k(G)\le 2f(q^{2}+q+10)$
is even, then [Reference Macdonald19] implies that $k(G)\le 2f(q^{2}+q+10)$![]() where $q=2^{f}$
where $q=2^{f}$![]() . Using the list of subgroups in [Reference Bray, Holt and Roney-Dougal2] this is enough to conclude that $q\leqslant 16$
. Using the list of subgroups in [Reference Bray, Holt and Roney-Dougal2] this is enough to conclude that $q\leqslant 16$![]() . Now [8] excludes the remainder.
. Now [8] excludes the remainder.
Finally, assume that $d=4$![]() . If $q$
. If $q$![]() is odd, then [Reference Macdonald19] implies that $k(G)\le 2f(q^{3}+q^{2}+5q+21)$
is odd, then [Reference Macdonald19] implies that $k(G)\le 2f(q^{3}+q^{2}+5q+21)$![]() where $q=p^{f}$
where $q=p^{f}$![]() . We use [Reference Kantor14] to conclude that $q=3$
. We use [Reference Kantor14] to conclude that $q=3$![]() . This final case is ruled out with [Reference Conway, Curtis, Norton, Parker and Wilson3]. If $q$
. This final case is ruled out with [Reference Conway, Curtis, Norton, Parker and Wilson3]. If $q$![]() is even, then [Reference Macdonald19] implies that $k(\mathrm {SL}_4(q))=q^{3}+q^{2}+q$
is even, then [Reference Macdonald19] implies that $k(\mathrm {SL}_4(q))=q^{3}+q^{2}+q$![]() and, again, we use the list of subgroups in [Reference Bray, Holt and Roney-Dougal2] to conclude that $q\leqslant 16$
and, again, we use the list of subgroups in [Reference Bray, Holt and Roney-Dougal2] to conclude that $q\leqslant 16$![]() . Now [Reference Bray, Holt and Roney-Dougal2, Reference Conway, Curtis, Norton, Parker and Wilson3, 8] rule out all except the listed exceptions for $q=2$
. Now [Reference Bray, Holt and Roney-Dougal2, Reference Conway, Curtis, Norton, Parker and Wilson3, 8] rule out all except the listed exceptions for $q=2$![]() .
.
Finally we deal with almost simple classical groups with socle $S$![]() not isomorphic to $\mathrm {PSL}_d(q)$
not isomorphic to $\mathrm {PSL}_d(q)$![]() . Note that to deal with this class of groups it is sufficient to consider $S=\mathrm {PSU}_d(q)$
. Note that to deal with this class of groups it is sufficient to consider $S=\mathrm {PSU}_d(q)$![]() with $d\geqslant 3$
with $d\geqslant 3$![]() and $(d,q)\neq (3,2)$
and $(d,q)\neq (3,2)$![]() ; $S=\mathrm {PSp}_d(q)$
; $S=\mathrm {PSp}_d(q)$![]() , with $d\geqslant 4$
, with $d\geqslant 4$![]() and $(d,q)\neq (4,2)$
and $(d,q)\neq (4,2)$![]() ; and $S=\mathrm {P\Omega }_d^{\varepsilon }(q)$
; and $S=\mathrm {P\Omega }_d^{\varepsilon }(q)$![]() with $d\geqslant 7$
with $d\geqslant 7$![]() .
.
Lemma 2.13 Let $G$![]() be almost simple with classical socle $S$
be almost simple with classical socle $S$![]() , $S\not \cong \mathrm {PSL}_d(q)$
, $S\not \cong \mathrm {PSL}_d(q)$![]() . Let $M$
. Let $M$![]() be a core-free maximal subgroup of $G$
be a core-free maximal subgroup of $G$![]() , and write $n=|G:M|$
, and write $n=|G:M|$![]() . If $k(G)\geqslant \frac {n}{2}$
. If $k(G)\geqslant \frac {n}{2}$![]() , then $G$
, then $G$![]() and $n$
and $n$![]() are listed in table 5.
are listed in table 5.
Table 5. Faithful primitive permutation representations of degree $n$![]() for almost simple classical groups $G$
for almost simple classical groups $G$![]() with socle $S\not \cong \mathrm {PSL}_d(q)$
with socle $S\not \cong \mathrm {PSL}_d(q)$![]() such that $k(G)\geqslant \frac {n}{2}$
such that $k(G)\geqslant \frac {n}{2}$![]()

Proof. In order to exclude some potential examples, our basic strategy will be to use the bound $k(G)\leqslant |G:S|k(S)$![]() from lemma 2.1, and try to show that this is smaller than $P(S)/2$
from lemma 2.1, and try to show that this is smaller than $P(S)/2$![]() . In order to bound $k(S)$
. In order to bound $k(S)$![]() , we will use the results in [Reference Fulman and Guralnick6] for specific families, as follows.
, we will use the results in [Reference Fulman and Guralnick6] for specific families, as follows.
Suppose that $S\cong \mathrm {PSU}_d(q)$![]() . In this case [Reference Fulman and Guralnick6, proposition 3.10] implies that $k(S)\leqslant 8.26q^{d-1}$
. In this case [Reference Fulman and Guralnick6, proposition 3.10] implies that $k(S)\leqslant 8.26q^{d-1}$![]() , and we use the values for $P(S)$
, and we use the values for $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12] to obtain that either $S$
given in [Reference Guest, Morris, Praeger and Spiga12] to obtain that either $S$![]() is in
is in
or else $d\leqslant 4$![]() . Groups with the five possible socles with $d>4$
. Groups with the five possible socles with $d>4$![]() can be ruled out using [8].
can be ruled out using [8].
If $S=\mathrm {PSU}_4(q)$![]() , then [Reference Macdonald19] implies that
, then [Reference Macdonald19] implies that

Thus, in any case, $k(G)\leqslant 2f(q^{3}+q^{2}+7q+23)$![]() where $q=p^{f}$
where $q=p^{f}$![]() . Since $P(S)=(q+1)(q^{3}+1)$
. Since $P(S)=(q+1)(q^{3}+1)$![]() , by [Reference Guest, Morris, Praeger and Spiga12], we conclude that $q\in \{2,3,4,5,8,16\}$
, by [Reference Guest, Morris, Praeger and Spiga12], we conclude that $q\in \{2,3,4,5,8,16\}$![]() . If $q\leqslant 5$
. If $q\leqslant 5$![]() , then [8] yields the listed cases. If $q\in \{8,16\}$
, then [8] yields the listed cases. If $q\in \{8,16\}$![]() , then $G=\mathrm {P\Gamma U}_4(q)$
, then $G=\mathrm {P\Gamma U}_4(q)$![]() . The case $q=8$
. The case $q=8$![]() is eliminated by [Reference Bosma, Cannon and Playoust1]; we now consider the case $q=16$
is eliminated by [Reference Bosma, Cannon and Playoust1]; we now consider the case $q=16$![]() . We want to apply lemma 2.2 with $G=\mathrm {P\Gamma U}_4(16)$
. We want to apply lemma 2.2 with $G=\mathrm {P\Gamma U}_4(16)$![]() and $N=\mathrm {SU}_4(16)$
and $N=\mathrm {SU}_4(16)$![]() . Consider the split torus $T$
. Consider the split torus $T$![]() of $N$
of $N$![]() of order $17^{3}$
of order $17^{3}$![]() , which intersects $284$
, which intersects $284$![]() nontrivial $N$
nontrivial $N$![]() -classes. By looking at eigenvalues, we see that none of these classes is fixed by the standard field automorphism $\sigma$
-classes. By looking at eigenvalues, we see that none of these classes is fixed by the standard field automorphism $\sigma$![]() of order $8$
of order $8$![]() normalizing $T$
normalizing $T$![]() . We deduce from lemma 2.2 that $k(G)\leqslant 8(q^{3}+q^{2}+3q+2 -284/2)=34080$
. We deduce from lemma 2.2 that $k(G)\leqslant 8(q^{3}+q^{2}+3q+2 -284/2)=34080$![]() , which is enough to conclude that $k(G)< P(S)/2$
, which is enough to conclude that $k(G)< P(S)/2$![]() .
.
If $G=\mathrm {PSU}_3(q)$![]() , then [Reference Macdonald19] implies that
, then [Reference Macdonald19] implies that

Thus, in any case, $k(G)\leqslant 2f(q^{2}+q+12)$![]() where $q=p^{f}$
where $q=p^{f}$![]() . Since $P(S)=q^{3}+1$
. Since $P(S)=q^{3}+1$![]() if $q\neq 5$
if $q\neq 5$![]() , by [Reference Guest, Morris, Praeger and Spiga12], we conclude that $q\leqslant 9$
, by [Reference Guest, Morris, Praeger and Spiga12], we conclude that $q\leqslant 9$![]() or $G=\mathrm {P\Gamma U}_3(16)$
or $G=\mathrm {P\Gamma U}_3(16)$![]() . For $q\leqslant 9$
. For $q\leqslant 9$![]() , we obtain the listed examples using [Reference Conway, Curtis, Norton, Parker and Wilson3, 8]. For $G=\mathrm {P\Gamma U}_3(16)$
, we obtain the listed examples using [Reference Conway, Curtis, Norton, Parker and Wilson3, 8]. For $G=\mathrm {P\Gamma U}_3(16)$![]() , the same argument used for the case $\mathrm {P\Gamma U}_4(16)$
, the same argument used for the case $\mathrm {P\Gamma U}_4(16)$![]() works.
works.
Suppose that $S\cong \mathrm {PSp}_d(q)$![]() . If $d\geqslant 6$
. If $d\geqslant 6$![]() , then we use [Reference Fulman and Guralnick6, theorems 3.12 and 3.13] along with the values for $P(S)$
, then we use [Reference Fulman and Guralnick6, theorems 3.12 and 3.13] along with the values for $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12] to conclude that $S$
given in [Reference Guest, Morris, Praeger and Spiga12] to conclude that $S$![]() is one of the following:
is one of the following:
We use [Reference Conway, Curtis, Norton, Parker and Wilson3, 8] to check these cases and obtain the listed examples.
If $S=\mathrm {PSp}_4(q)$![]() , then we use [Reference Wall26] (for $q$
, then we use [Reference Wall26] (for $q$![]() odd) and [Reference Enomoto5] (for $q$
odd) and [Reference Enomoto5] (for $q$![]() even) to establish that
even) to establish that

This, combined with [Reference Guest, Morris, Praeger and Spiga12], implies that $q\leqslant 9$![]() . Now [Reference Conway, Curtis, Norton, Parker and Wilson3, 8] yield the listed examples.
. Now [Reference Conway, Curtis, Norton, Parker and Wilson3, 8] yield the listed examples.
Suppose that $S\cong \mathrm {P\Omega }_{2\ell +1}(q)$![]() . Here we assume that $\ell \geqslant 3$
. Here we assume that $\ell \geqslant 3$![]() and that $q$
and that $q$![]() is odd. Now [Reference Fulman and Guralnick6, theorem 3.19] along with the values for $P(S)$
is odd. Now [Reference Fulman and Guralnick6, theorem 3.19] along with the values for $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12] imply that $S=\mathrm {P\Omega }_7(3)$
given in [Reference Guest, Morris, Praeger and Spiga12] imply that $S=\mathrm {P\Omega }_7(3)$![]() . This final case can be excluded using [Reference Conway, Curtis, Norton, Parker and Wilson3].
. This final case can be excluded using [Reference Conway, Curtis, Norton, Parker and Wilson3].
Suppose that $S\cong \mathrm {P\Omega }^{\pm } _{2\ell }(q)$![]() with $q$
with $q$![]() odd. We make use of [Reference Fulman and Guralnick6, theorems 3.16 and 3.18] along with the values for $P(S)$
odd. We make use of [Reference Fulman and Guralnick6, theorems 3.16 and 3.18] along with the values for $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12] to obtain that
given in [Reference Guest, Morris, Praeger and Spiga12] to obtain that
In $\mathrm {P\Omega }_8^{+}(5)$![]() and $\mathrm {P\Omega }_8^{+}(7)$
and $\mathrm {P\Omega }_8^{+}(7)$![]() , the outer automorphism group is $S_4$
, the outer automorphism group is $S_4$![]() , and a subgroup of $S_4$
, and a subgroup of $S_4$![]() has at most $5$
has at most $5$![]() conjugacy classes, therefore by lemma 2.1 we get $k(G)\leqslant 5k(S)$
conjugacy classes, therefore by lemma 2.1 we get $k(G)\leqslant 5k(S)$![]() , which is enough to rule out these possibilities.
, which is enough to rule out these possibilities.
We use [Reference Bosma, Cannon and Playoust1, 8] to rule out the cases where $S=\mathrm {P\Omega }_{10}^{\pm }(3)$![]() or $\mathrm {P\Omega }_8^{\pm }(3)$
or $\mathrm {P\Omega }_8^{\pm }(3)$![]() .
.
Suppose that $S\cong \Omega ^{\pm } _{2\ell }(q)$![]() with $q$
with $q$![]() even. We make use of [Reference Fulman and Guralnick6, theorem 3.22] along with the values for $P(S)$
even. We make use of [Reference Fulman and Guralnick6, theorem 3.22] along with the values for $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12] to obtain that
given in [Reference Guest, Morris, Praeger and Spiga12] to obtain that
We use [Reference Conway, Curtis, Norton, Parker and Wilson3] for the groups with $q=2$![]() , and we get the listed examples. We can rule out $\Omega _8^{+}(4)$
, and we get the listed examples. We can rule out $\Omega _8^{+}(4)$![]() using [Reference Bosma, Cannon and Playoust1].
using [Reference Bosma, Cannon and Playoust1].
2.5 Proof of theorem 1.2
Let $G$![]() be an almost simple primitive permutation group of degree $n$
be an almost simple primitive permutation group of degree $n$![]() . Putting together lemmas 2.3, 2.8, 2.11, 2.12 and 2.13, we get that either $k(G)< n/2$
. Putting together lemmas 2.3, 2.8, 2.11, 2.12 and 2.13, we get that either $k(G)< n/2$![]() , or we are in case (2) of theorem 1.2 (regarding table 1, recall remark 1.3(iii)).
, or we are in case (2) of theorem 1.2 (regarding table 1, recall remark 1.3(iii)).
Note that, if the action of $G$![]() is isomorphic to an action in (B), then $k(G)<100n$
is isomorphic to an action in (B), then $k(G)<100n$![]() follows immediately from theorem 2.10.
follows immediately from theorem 2.10.
It remains to prove the asymptotic statement, that is, either $k(G)=O(n^{3/4})$![]() , or the action of $G$
, or the action of $G$![]() is isomorphic to an action in (A) or (B). We assume that this latter condition does not hold, and we want to show $k(G)=O(n^{3/4})$
is isomorphic to an action in (A) or (B). We assume that this latter condition does not hold, and we want to show $k(G)=O(n^{3/4})$![]() .
.
We may assume that $G$![]() is sufficiently large along the proof. Let $M$
is sufficiently large along the proof. Let $M$![]() be the stabilizer of a point in the action of $G$
be the stabilizer of a point in the action of $G$![]() on $n$
on $n$![]() points; in particular $|G:M|=n$
points; in particular $|G:M|=n$![]() . Write $S=\mathrm {Soc}(G)$
. Write $S=\mathrm {Soc}(G)$![]() .
.
Assume first that $S\cong A_d$![]() , and assume that $M$
, and assume that $M$![]() is transitive on $d$
is transitive on $d$![]() points; we will show that $k(G)=n^{o(1)}$
points; we will show that $k(G)=n^{o(1)}$![]() as $d$
as $d$![]() tends to infinity. By lemma 2.4 (or by the Hardy–Ramanujan asymptotic formula), we have $k(G)=O(1)^{\sqrt d}$
tends to infinity. By lemma 2.4 (or by the Hardy–Ramanujan asymptotic formula), we have $k(G)=O(1)^{\sqrt d}$![]() . On the other hand, by lemmas 2.5 and 2.6, if $M$
. On the other hand, by lemmas 2.5 and 2.6, if $M$![]() is primitive on $d$
is primitive on $d$![]() points then $n\geqslant (d/O(1))^{d}$
points then $n\geqslant (d/O(1))^{d}$![]() ; and by (2.1) in the proof of lemma 2.8, if $M$
; and by (2.1) in the proof of lemma 2.8, if $M$![]() is imprimitive then $n\geqslant c^{d}$
is imprimitive then $n\geqslant c^{d}$![]() for some constant $c$
for some constant $c$![]() . Therefore $k(G)=n^{o(1)}$
. Therefore $k(G)=n^{o(1)}$![]() if $S\cong A_d$
if $S\cong A_d$![]() .
.
Assume now that $S\cong \mathrm {PSL}_d(q)$![]() . We have $k(G)=O(q^{d-1})$
. We have $k(G)=O(q^{d-1})$![]() by theorem 2.10. If $H:=M\cap \mathrm {P\Gamma L}_d(q)$
by theorem 2.10. If $H:=M\cap \mathrm {P\Gamma L}_d(q)$![]() is reducible in the action on $\mathbf {F}_q^{d}$
is reducible in the action on $\mathbf {F}_q^{d}$![]() , one possibility is that it stabilizes a $k$
, one possibility is that it stabilizes a $k$![]() -space for some $2\leqslant k \leqslant d-2$
-space for some $2\leqslant k \leqslant d-2$![]() , and so $n> q^{2d-4}$
, and so $n> q^{2d-4}$![]() . If $d\rightarrow \infty$
. If $d\rightarrow \infty$![]() , we see that $k(G)=o(n^{3/4})$
, we see that $k(G)=o(n^{3/4})$![]() ; and if $d$
; and if $d$![]() is bounded, we see that $k(G)=O(n^{3/4})$
is bounded, we see that $k(G)=O(n^{3/4})$![]() (we actually have $k(G)=o(n^{3/4})$
(we actually have $k(G)=o(n^{3/4})$![]() as $q\rightarrow \infty$
as $q\rightarrow \infty$![]() except for the case $(d,k)=(4,2)$
except for the case $(d,k)=(4,2)$![]() ). The remaining possibility is that $G\nleq \mathrm {P\Gamma L}_d(q)$
). The remaining possibility is that $G\nleq \mathrm {P\Gamma L}_d(q)$![]() and $M$
and $M$![]() is the stabilizer of a flag (pair of incident point-hyperplane) or antiflag (pair of complementary point-hyperplane). But in this case $n>q^{2d-3}$
is the stabilizer of a flag (pair of incident point-hyperplane) or antiflag (pair of complementary point-hyperplane). But in this case $n>q^{2d-3}$![]() , and the previous computation is sufficient for $d\geqslant 4$
, and the previous computation is sufficient for $d\geqslant 4$![]() ; and for $d=3$
; and for $d=3$![]() , $k(G)=O(n^{2/3})$
, $k(G)=O(n^{2/3})$![]() .
.
If $d=2m\geqslant 4$![]() and $H$
and $H$![]() normalizes $\mathrm {PSp}_{2m}(q)$
normalizes $\mathrm {PSp}_{2m}(q)$![]() , then
, then
and we can easily check that $k(G)=O(q^{d-1}) = o(n^{3/4})$![]() .
.
If now $H$![]() is irreducible and does not normalize $\mathrm {PSp}_d(q)$
is irreducible and does not normalize $\mathrm {PSp}_d(q)$![]() , we can apply the main theorem of [Reference Kantor14]. We see easily that $k(G)=o(n^{3/4})$
, we can apply the main theorem of [Reference Kantor14]. We see easily that $k(G)=o(n^{3/4})$![]() as $d\rightarrow \infty$
as $d\rightarrow \infty$![]() . If $d$
. If $d$![]() is bounded instead, then we can assume that $q$
is bounded instead, then we can assume that $q$![]() is large and in particular [Reference Kantor14] implies that $n\geqslant q^{(d-1)(d-2)/2}$
is large and in particular [Reference Kantor14] implies that $n\geqslant q^{(d-1)(d-2)/2}$![]() , which proves $k(G)=o(n^{3/4})$
, which proves $k(G)=o(n^{3/4})$![]() in case $d\geqslant 5$
in case $d\geqslant 5$![]() . In case $d\leqslant 4$
. In case $d\leqslant 4$![]() , we can use the list of maximal subgroups of $\mathrm {PSL}_d(q)$
, we can use the list of maximal subgroups of $\mathrm {PSL}_d(q)$![]() given in [Reference Bray, Holt and Roney-Dougal2] in order to prove $k(G)=o(n^{3/4})$
given in [Reference Bray, Holt and Roney-Dougal2] in order to prove $k(G)=o(n^{3/4})$![]() (if $H$
(if $H$![]() is irreducible, $n\gg q^{3/2}$
is irreducible, $n\gg q^{3/2}$![]() for $d=2$
for $d=2$![]() ; $n\gg q^{4}$
; $n\gg q^{4}$![]() for $d=3$
for $d=3$![]() ; and $n\gg q^{5}$
; and $n\gg q^{5}$![]() for $d=4$
for $d=4$![]() ).
).
Assume finally that $S$![]() is a group of Lie type and that $S\not \cong \mathrm {PSL}_d(q)$
is a group of Lie type and that $S\not \cong \mathrm {PSL}_d(q)$![]() . In this case we want to show $k(G) = O(P(S)^{3/4})$
. In this case we want to show $k(G) = O(P(S)^{3/4})$![]() , which implies the statement, since $P(S)\leqslant n$
, which implies the statement, since $P(S)\leqslant n$![]() . This can be checked combining $k(G)=O(q^{r})$
. This can be checked combining $k(G)=O(q^{r})$![]() (where $r$
(where $r$![]() is the untwisted rank of $S$
is the untwisted rank of $S$![]() ) with the value of $P(S)$
) with the value of $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12]. In fact, we get $k(G) = o(P(S)^{3/4})$
given in [Reference Guest, Morris, Praeger and Spiga12]. In fact, we get $k(G) = o(P(S)^{3/4})$![]() unless $S\cong \mathrm {PSU}_4(q)$
unless $S\cong \mathrm {PSU}_4(q)$![]() . (We remark that, in the latter case, $P(S)$
. (We remark that, in the latter case, $P(S)$![]() is equal to the number of totally singular $2$
is equal to the number of totally singular $2$![]() -subspaces of $\mathbf {F}_{q^{2}}^{4}$
-subspaces of $\mathbf {F}_{q^{2}}^{4}$![]() ; we also use [Reference Bray, Holt and Roney-Dougal2] in order to see that $n\gg q^{5}$
; we also use [Reference Bray, Holt and Roney-Dougal2] in order to see that $n\gg q^{5}$![]() for every other primitive action of $G$
for every other primitive action of $G$![]() .)
.)
This concludes the proof of theorem 1.2.
Remark 2.14 In theorem 1.2(1), we actually showed that $k(G)=o(n^{3/4})$![]() as $n\rightarrow \infty$
as $n\rightarrow \infty$![]() unless $S\cong \mathrm {PSL}_4(q)$
unless $S\cong \mathrm {PSL}_4(q)$![]() and $G$
and $G$![]() acts on the set of $2$
acts on the set of $2$![]() -subspaces of $\mathbf {F}_q^{4}$
-subspaces of $\mathbf {F}_q^{4}$![]() , or $S\cong \mathrm {PSU}_4(q)$
, or $S\cong \mathrm {PSU}_4(q)$![]() and $G$
and $G$![]() acts on the set of totally singular $2$
acts on the set of totally singular $2$![]() -subspaces of $\mathbf {F}_{q^{2}}^{4}$
-subspaces of $\mathbf {F}_{q^{2}}^{4}$![]() . In these cases, we have $n\sim q^{4}$
. In these cases, we have $n\sim q^{4}$![]() and $k(S)\asymp q^{3}$
and $k(S)\asymp q^{3}$![]() , therefore $k(S)\asymp n^{3/4}$
, therefore $k(S)\asymp n^{3/4}$![]() . (Recall that $f\asymp g$
. (Recall that $f\asymp g$![]() means that $c_1f\leqslant g\leqslant c_2f$
means that $c_1f\leqslant g\leqslant c_2f$![]() for positive constants $c_1$
for positive constants $c_1$![]() and $c_2$
and $c_2$![]() .)
.)
3. The general case
In this section we prove theorem 1.1. We first prove a lemma.
Lemma 3.1 Let $G$![]() be a finite almost simple group with socle $S$
be a finite almost simple group with socle $S$![]() . Then either $S\cong A_5, A_6, \mathrm {PSL}_2(7), \mathrm {PSL}_2(11)$
. Then either $S\cong A_5, A_6, \mathrm {PSL}_2(7), \mathrm {PSL}_2(11)$![]() , or $4\cdot k(G)^{2} < |S|$
, or $4\cdot k(G)^{2} < |S|$![]() . Moreover, $k(G)^{3} =O(|S|)$
. Moreover, $k(G)^{3} =O(|S|)$![]() .
.
We note that we actually have $k(G)^{3}=o(|S|)$![]() as $|S|\rightarrow \infty$
as $|S|\rightarrow \infty$![]() , except for the case $S\cong \mathrm {PSL}_2(q)$
, except for the case $S\cong \mathrm {PSL}_2(q)$![]() .
.
Proof. We first prove $4\cdot k(G)^{2} < |S|$![]() , with the listed exceptions.
, with the listed exceptions.
Assume first that $S\cong A_d$![]() . Then lemmas 2.4, 2.5 and a straightforward computation imply that it is sufficient to show
. Then lemmas 2.4, 2.5 and a straightforward computation imply that it is sufficient to show
which is true for $d\geqslant 10$![]() . For $d\leqslant 9$
. For $d\leqslant 9$![]() , direct check gives the exceptions in the statement.
, direct check gives the exceptions in the statement.
Assume now that $S\cong \mathrm {PSL}_d(q)$![]() . Using the bound $k(S)\leqslant 2.5 q^{d-1}$
. Using the bound $k(S)\leqslant 2.5 q^{d-1}$![]() from [Reference Fulman and Guralnick6], lemma 2.1, and the fact that $|G:S|\leqslant 2f(d,q-1)$
from [Reference Fulman and Guralnick6], lemma 2.1, and the fact that $|G:S|\leqslant 2f(d,q-1)$![]() , with $q=p^{f}$
, with $q=p^{f}$![]() , we see that it is sufficient to show
, we see that it is sufficient to show
If $d\geqslant 4$![]() , we can easily verify that this is true. For $d=3$
, we can easily verify that this is true. For $d=3$![]() , [Reference Macdonald19] tells us that $k(S)\leqslant q^{2}+q$
, [Reference Macdonald19] tells us that $k(S)\leqslant q^{2}+q$![]() . We compute that it is enough to show
. We compute that it is enough to show
which can be verified unless $q=2,4$![]() . The case $q=2$
. The case $q=2$![]() is in the statement (since $\mathrm {SL}_3(2) \cong \mathrm {PSL}_2(7)$
is in the statement (since $\mathrm {SL}_3(2) \cong \mathrm {PSL}_2(7)$![]() ), while the case $q=4$
), while the case $q=4$![]() can be excluded with [8].
can be excluded with [8].
If $d=2$![]() , we use the exact value of $k(S)$
, we use the exact value of $k(S)$![]() (recalled in the proof of lemma 2.12), in order to reduce to the cases $q\leqslant 16$
(recalled in the proof of lemma 2.12), in order to reduce to the cases $q\leqslant 16$![]() or $q=25,27,32,64,81,128,256$
or $q=25,27,32,64,81,128,256$![]() . Then we use [8] and we get the cases $q=4,5,7,9,11$
. Then we use [8] and we get the cases $q=4,5,7,9,11$![]() in the statement.
in the statement.
Assume that $S$![]() is classical and that $S\not \cong \mathrm {PSL}_d(q)$
is classical and that $S\not \cong \mathrm {PSL}_d(q)$![]() . Here one can prove that $4k(G)^{2} < |S|$
. Here one can prove that $4k(G)^{2} < |S|$![]() using the upper bounds for $k(S)$
using the upper bounds for $k(S)$![]() given in [Reference Fulman and Guralnick6]. One can also argue as follows (but this is not necessary). If $G$
given in [Reference Fulman and Guralnick6]. One can also argue as follows (but this is not necessary). If $G$![]() appears in table 1, we can make a direct check. If $G$
appears in table 1, we can make a direct check. If $G$![]() is not in table 1, then theorem 1.2 tells us that $k(G)< P_m(G)/2$
is not in table 1, then theorem 1.2 tells us that $k(G)< P_m(G)/2$![]() , where $P_m(G)$
, where $P_m(G)$![]() denotes the smallest index of a core-free maximal subgroup of $G$
denotes the smallest index of a core-free maximal subgroup of $G$![]() . Now it is known (see [Reference Kleidman and Liebeck15, p. 178]) that $P(S)\leqslant |S|^{1/2}$
. Now it is known (see [Reference Kleidman and Liebeck15, p. 178]) that $P(S)\leqslant |S|^{1/2}$![]() . In particular, whenever $P_m(G)=P(S)$
. In particular, whenever $P_m(G)=P(S)$![]() , we can immediately conclude $4k(G)^{2} < |S|$
, we can immediately conclude $4k(G)^{2} < |S|$![]() . Certainly we have $P(S)\leqslant P_m(G)$
. Certainly we have $P(S)\leqslant P_m(G)$![]() . Using the value of $P(S)$
. Using the value of $P(S)$![]() given in [Reference Guest, Morris, Praeger and Spiga12] (see also [Reference Cooperstein4], where an explicit $M$
given in [Reference Guest, Morris, Praeger and Spiga12] (see also [Reference Cooperstein4], where an explicit $M$![]() for which $|S:M|=P(S)$
for which $|S:M|=P(S)$![]() is given), and consulting [Reference Kleidman and Liebeck15], we deduce that $P_m(G)=P(S)$
is given), and consulting [Reference Kleidman and Liebeck15], we deduce that $P_m(G)=P(S)$![]() unless $S\cong \mathrm {PSU}_3(5)$
unless $S\cong \mathrm {PSU}_3(5)$![]() , $S\cong \mathrm {Sp}_4(q)$
, $S\cong \mathrm {Sp}_4(q)$![]() with $q$
with $q$![]() even, $S\cong \mathrm {P\Omega }_8^{+}(q)$
even, $S\cong \mathrm {P\Omega }_8^{+}(q)$![]() , or $S\cong \mathrm {P\Omega }^{+}_{2m}(3)$
, or $S\cong \mathrm {P\Omega }^{+}_{2m}(3)$![]() with $m\geqslant 4$
with $m\geqslant 4$![]() . (If $S\cong \mathrm {PSU}_3(5)$
. (If $S\cong \mathrm {PSU}_3(5)$![]() , $|S:M|=P(S)$
, $|S:M|=P(S)$![]() where $M$
where $M$![]() is isomorphic to $A_7$
is isomorphic to $A_7$![]() ; if $S\cong \mathrm {P\Omega }^{+}_{2m}(3)$
; if $S\cong \mathrm {P\Omega }^{+}_{2m}(3)$![]() , $M$
, $M$![]() is the stabilizer of a nondegenerate $1$
is the stabilizer of a nondegenerate $1$![]() -space.) We can exclude the unitary case with [Reference Conway, Curtis, Norton, Parker and Wilson3]; in the symplectic case we can use $k(\mathrm {Sp}_4(q))=q^{2}+2q+3$
-space.) We can exclude the unitary case with [Reference Conway, Curtis, Norton, Parker and Wilson3]; in the symplectic case we can use $k(\mathrm {Sp}_4(q))=q^{2}+2q+3$![]() (see the proof of lemma 2.13); in the orthogonal cases we can use the bound $k(\mathrm {P\Omega }_{2m}^{+}(q))\leqslant 14q^{m}$
(see the proof of lemma 2.13); in the orthogonal cases we can use the bound $k(\mathrm {P\Omega }_{2m}^{+}(q))\leqslant 14q^{m}$![]() given in [Reference Fulman and Guralnick6].
given in [Reference Fulman and Guralnick6].
Assume that $S$![]() is exceptional. In the proof of lemma 2.11 we actually proved $k(G)< P(S)/2$
is exceptional. In the proof of lemma 2.11 we actually proved $k(G)< P(S)/2$![]() , therefore we conclude by the argument of the previous paragraph.
, therefore we conclude by the argument of the previous paragraph.
Assume finally that $S$![]() is sporadic. We use [Reference Conway, Curtis, Norton, Parker and Wilson3] to conclude $4k(G)^{2}<|S|$
is sporadic. We use [Reference Conway, Curtis, Norton, Parker and Wilson3] to conclude $4k(G)^{2}<|S|$![]() .
.
It remains to prove the asymptotic statement, that is, $k(G)^{3} =O(|S|)$![]() (and indeed $k(G)^{3} =o(|S|)$
(and indeed $k(G)^{3} =o(|S|)$![]() if $S\not \cong \mathrm {PSL}_2(q)$
if $S\not \cong \mathrm {PSL}_2(q)$![]() ). We may assume that $S$
). We may assume that $S$![]() is sufficiently large, and the statement is easy to check, using lemma 2.4 and theorem 2.10.
is sufficiently large, and the statement is easy to check, using lemma 2.4 and theorem 2.10.
We need three technical lemmas.
Lemma 3.2 Assume that $S\cong A_d$![]() , or that $S$
, or that $S$![]() is the socle of some group appearing in table 1. If $S\leqslant B\leqslant A\leqslant \mathrm {Aut}(S)$
is the socle of some group appearing in table 1. If $S\leqslant B\leqslant A\leqslant \mathrm {Aut}(S)$![]() , then $k(B)\leqslant k(A)$
, then $k(B)\leqslant k(A)$![]() , unless $A=\Omega ^{+}_8(2).S_3$
, unless $A=\Omega ^{+}_8(2).S_3$![]() .
.
Proof. If $S\cong A_d$![]() , the statement follows from lemma 2.7, and by direct check in case $d=6$
, the statement follows from lemma 2.7, and by direct check in case $d=6$![]() . If $S$
. If $S$![]() is the socle of some group appearing in table 1, we use [Reference Conway, Curtis, Norton, Parker and Wilson3].
is the socle of some group appearing in table 1, we use [Reference Conway, Curtis, Norton, Parker and Wilson3].
Lemma 3.3 Assume that $G$![]() is almost simple with socle $S\cong \mathrm {PSL}_d(q)$
is almost simple with socle $S\cong \mathrm {PSL}_d(q)$![]() , with $d\geqslant 3$
, with $d\geqslant 3$![]() , and let $m$
, and let $m$![]() denote the number of flags (that is, pairs of incident point-hyperplane) in $\mathbf {F}_q^{d}$
denote the number of flags (that is, pairs of incident point-hyperplane) in $\mathbf {F}_q^{d}$![]() . Then, $k(G)< m/2$
. Then, $k(G)< m/2$![]() and $k(G)=O(m^{2/3})$
and $k(G)=O(m^{2/3})$![]() .
.
We note that we actually have $k(G)=o(m^{2/3})$![]() as $m\rightarrow \infty$
as $m\rightarrow \infty$![]() , except in case $d=3$
, except in case $d=3$![]() .
.
Proof. We begin with the inequality $k(G)< m/2$![]() . If $G\nleq \mathrm {P\Gamma L}_d(q)$
. If $G\nleq \mathrm {P\Gamma L}_d(q)$![]() , then $G$
, then $G$![]() acts primitively on the set of flags, and the statement follows from theorem 1.2. Assume now that $G\leqslant \mathrm {P\Gamma L}_d(q)$
acts primitively on the set of flags, and the statement follows from theorem 1.2. Assume now that $G\leqslant \mathrm {P\Gamma L}_d(q)$![]() . Then $G$
. Then $G$![]() acts primitively on the set of $2$
acts primitively on the set of $2$![]() -subspaces of $\mathbf {F}_q^{d}$
-subspaces of $\mathbf {F}_q^{d}$![]() . It is easy to see that the number of $2$
. It is easy to see that the number of $2$![]() -subspaces is smaller than the number of flags. Assume that $d\geqslant 4$
-subspaces is smaller than the number of flags. Assume that $d\geqslant 4$![]() . Then, by lemma 2.12, either $k(G)< m/2$
. Then, by lemma 2.12, either $k(G)< m/2$![]() , or $G$
, or $G$![]() appears in table 4. Examining table 4, we see that $k(G)< m/2$
appears in table 4. Examining table 4, we see that $k(G)< m/2$![]() also in the latter case.
also in the latter case.
We are left with the case $d=3$![]() . We have $k(G)\leqslant 100q^{2}$
. We have $k(G)\leqslant 100q^{2}$![]() by theorem 2.10, and moreover $m>q^{3}$
by theorem 2.10, and moreover $m>q^{3}$![]() . In particular, if $k(G)\geqslant m/2$
. In particular, if $k(G)\geqslant m/2$![]() then $q<200$
then $q<200$![]() . We whittle down a bit the possibilities. Write $a=(3,q-1)$
. We whittle down a bit the possibilities. Write $a=(3,q-1)$![]() . By [Reference Macdonald19] and lemma 2.1, we deduce $k(G)\leqslant |G:S|\cdot (q^{2}+q+5a-5)/a < 2|G:S|\cdot q^{2}$
. By [Reference Macdonald19] and lemma 2.1, we deduce $k(G)\leqslant |G:S|\cdot (q^{2}+q+5a-5)/a < 2|G:S|\cdot q^{2}$![]() . Therefore, if $q=p^{f}$
. Therefore, if $q=p^{f}$![]() , we have $q<8af$
, we have $q<8af$![]() . Using $q<200$
. Using $q<200$![]() , we see that we are reduced to the cases $q\leqslant 27$
, we see that we are reduced to the cases $q\leqslant 27$![]() and $q=32,64$
and $q=32,64$![]() , which can be checked with [8] (if $q\neq 2,4,8,16$
, which can be checked with [8] (if $q\neq 2,4,8,16$![]() , it is enough to show that $4f(q^{2}+q+5a-5)$
, it is enough to show that $4f(q^{2}+q+5a-5)$![]() is smaller than $m$
is smaller than $m$![]() , without computing the actual value of $k(G)$
, without computing the actual value of $k(G)$![]() ).
).
The asymptotic statement $k(G)=O(m^{2/3})$![]() can be checked easily using $k(G)=O(q^{d-1})$
can be checked easily using $k(G)=O(q^{d-1})$![]() .
.
Lemma 3.4 Let $A$![]() be an almost simple primitive group of degree $m$
be an almost simple primitive group of degree $m$![]() with socle $S$
with socle $S$![]() , and assume that $A$
, and assume that $A$![]() is not in the possibilities of theorem 1.2(2). Let $S\leqslant B\leqslant A$
is not in the possibilities of theorem 1.2(2). Let $S\leqslant B\leqslant A$![]() . Then, $k(B)< m/2$
. Then, $k(B)< m/2$![]() . Moreover, for every fixed $\alpha > 3/4$
. Moreover, for every fixed $\alpha > 3/4$![]() , if $S$
, if $S$![]() is sufficiently large then $k(B)< m^{\alpha }$
is sufficiently large then $k(B)< m^{\alpha }$![]() .
.
Proof. We begin with the inequality $k(B)< m/2$![]() . Write $m=|A:M|$
. Write $m=|A:M|$![]() for some core-free maximal subgroup $M$
for some core-free maximal subgroup $M$![]() of $A$
of $A$![]() . If $B=A$
. If $B=A$![]() , the claim is true by theorem 1.2. Assume, for a contradiction, that there exists $B$
, the claim is true by theorem 1.2. Assume, for a contradiction, that there exists $B$![]() such that $k(B)\geqslant m/2=|B:B\cap M|/2$
such that $k(B)\geqslant m/2=|B:B\cap M|/2$![]() . Let $T$
. Let $T$![]() be a core-free subgroup of $B$
be a core-free subgroup of $B$![]() , maximal with respect to the property that $B\cap M\leqslant T$
, maximal with respect to the property that $B\cap M\leqslant T$![]() and that $T$
and that $T$![]() is core-free in $B$
is core-free in $B$![]() (that is, $T$
(that is, $T$![]() does not contain $S$
does not contain $S$![]() ).
).
Note that, by the maximality of $T$![]() , the subgroups of $B$
, the subgroups of $B$![]() properly containing $T$
properly containing $T$![]() must contain $S$
must contain $S$![]() . Then choose $C$
. Then choose $C$![]() such that $T< C\leqslant B$
such that $T< C\leqslant B$![]() and $T$
and $T$![]() is maximal in $C$
is maximal in $C$![]() . In particular, $C$
. In particular, $C$![]() acts primitively on the cosets of $T$
acts primitively on the cosets of $T$![]() , and moreover, by lemma 2.1,
, and moreover, by lemma 2.1,
whence $k(C)\geqslant |C:T|/2$![]() . Therefore we can apply theorem 1.2. The first possibility is that $C$
. Therefore we can apply theorem 1.2. The first possibility is that $C$![]() appears in table 1. By lemma 3.2 and $k(B)\geqslant m/2$
appears in table 1. By lemma 3.2 and $k(B)\geqslant m/2$![]() , we deduce $A=\Omega ^{+}_8(2).S_3$
, we deduce $A=\Omega ^{+}_8(2).S_3$![]() . Then by [Reference Conway, Curtis, Norton, Parker and Wilson3] $m\geqslant 3600$
. Then by [Reference Conway, Curtis, Norton, Parker and Wilson3] $m\geqslant 3600$![]() , which contradicts $k(B)\geqslant m/2$
, which contradicts $k(B)\geqslant m/2$![]() . By lemma 3.2, we also see that it cannot be $S\cong A_d$
. By lemma 3.2, we also see that it cannot be $S\cong A_d$![]() . By theorem 1.2 and lemma 2.12, the only remaining possibility is that $S\cong \mathrm {PSL}_d(q)$
. By theorem 1.2 and lemma 2.12, the only remaining possibility is that $S\cong \mathrm {PSL}_d(q)$![]() , $C\leqslant \mathrm {P\Gamma L}_d(q)$
, $C\leqslant \mathrm {P\Gamma L}_d(q)$![]() and $T$
and $T$![]() is the stabilizer of a $1$
is the stabilizer of a $1$![]() -space or $(d-1)$
-space or $(d-1)$![]() -space. In particular, $B\cap M$
-space. In particular, $B\cap M$![]() stabilizes a $1$
stabilizes a $1$![]() -space or a $(d-1)$
-space or a $(d-1)$![]() -space.
-space.
Assume first that $A\leqslant \mathrm {P\Gamma L}_d(q)$![]() . By assumption, $M$
. By assumption, $M$![]() is not the stabilizer of a $1$
is not the stabilizer of a $1$![]() -space or $(d-1)$
-space or $(d-1)$![]() -space. Then, there is no other possibility for $M$
-space. Then, there is no other possibility for $M$![]() (in such a way that $B\cap M$
(in such a way that $B\cap M$![]() fixes a $1$
fixes a $1$![]() -space or $(d-1)$
-space or $(d-1)$![]() -space), which is a contradiction. Assume finally that $A\nleq \mathrm {P\Gamma L}_d(q)$
-space), which is a contradiction. Assume finally that $A\nleq \mathrm {P\Gamma L}_d(q)$![]() . Then the only possibility is that $M$
. Then the only possibility is that $M$![]() is the stabilizer of a flag or antiflag. In particular, $m$
is the stabilizer of a flag or antiflag. In particular, $m$![]() is larger than the number of flags in $\mathbf {F}_q^{d}$
is larger than the number of flags in $\mathbf {F}_q^{d}$![]() , which contradicts lemma 3.3. This final contradiction proves that $k(B)< m/2$
, which contradicts lemma 3.3. This final contradiction proves that $k(B)< m/2$![]() for every $S\leqslant B\leqslant A$
for every $S\leqslant B\leqslant A$![]() .
.
Now we want to show that, for every fixed $\alpha >3/4$![]() , if $S$
, if $S$![]() is sufficiently large then $k(B)< m^{\alpha }$
is sufficiently large then $k(B)< m^{\alpha }$![]() for every $S\leqslant B\leqslant A$
for every $S\leqslant B\leqslant A$![]() .
.
By theorem 1.2, we have $k(A)=O(m^{3/4})$![]() . Assume that $k(B)\geqslant m^{\alpha }$
. Assume that $k(B)\geqslant m^{\alpha }$![]() . We want to show that $S$
. We want to show that $S$![]() has bounded order (in other words, we want to show that, if $S$
has bounded order (in other words, we want to show that, if $S$![]() is sufficiently large, we get a contradiction). By taking $S$
is sufficiently large, we get a contradiction). By taking $S$![]() large, we have $k(B)>k(A)$
large, we have $k(B)>k(A)$![]() . Much of the argument of the first part of the proof carries unchanged, except that we have the inequality
. Much of the argument of the first part of the proof carries unchanged, except that we have the inequality
from which $k(C)\geqslant |C:T|^{\alpha } \cdot |B:C|^{\alpha -1}$![]() . Note that $|B:C|\leqslant |\mathrm {Out}(S)|$
. Note that $|B:C|\leqslant |\mathrm {Out}(S)|$![]() and $|C:T|\geqslant P(S)$
and $|C:T|\geqslant P(S)$![]() . Using [Reference Guest, Morris, Praeger and Spiga12, table 4], we easily see that $|\mathrm {Out}(S)|=P(S)^{o(1)}$
. Using [Reference Guest, Morris, Praeger and Spiga12, table 4], we easily see that $|\mathrm {Out}(S)|=P(S)^{o(1)}$![]() as $|S|\rightarrow \infty$
as $|S|\rightarrow \infty$![]() (the statement being obvious in case $S\cong A_d$
(the statement being obvious in case $S\cong A_d$![]() ), from which we get that, for every fixed $\beta <\alpha$
), from which we get that, for every fixed $\beta <\alpha$![]() ,
,
if $S$![]() is sufficiently large. In particular we may take $\beta >3/4$
is sufficiently large. In particular we may take $\beta >3/4$![]() , and by theorem 1.2, we deduce that $C$
, and by theorem 1.2, we deduce that $C$![]() and $|C:T|$
and $|C:T|$![]() must appear in item (2) of the theorem. Then, the argument that we used in the first part of the proof, together with lemma 3.3, gives a contradiction.
must appear in item (2) of the theorem. Then, the argument that we used in the first part of the proof, together with lemma 3.3, gives a contradiction.
3.1 Proof of theorem 1.1
We can now prove theorem 1.1. We will apply many times lemma 2.1, usually with no mention. Moreover, we will often use the following theorem from [Reference Liebeck and Pyber17], which we recalled in the introduction.
Theorem 3.5 Let $r\geqslant 1$![]() and let $P\leqslant S_r$
and let $P\leqslant S_r$![]() . Then, $k(P)\leqslant 2^{r-1}$
. Then, $k(P)\leqslant 2^{r-1}$![]() .
.
Let $G$![]() be a primitive permutation group of degree $n$
be a primitive permutation group of degree $n$![]() with nonabelian socle $\mathrm {Soc}(G)\cong S^{r}$
with nonabelian socle $\mathrm {Soc}(G)\cong S^{r}$![]() , with $S$
, with $S$![]() simple.
simple.
In the following proof, a permutation group $G$![]() of degree $n$
of degree $n$![]() in product action refers to a group $G\leqslant A\wr S_r$
in product action refers to a group $G\leqslant A\wr S_r$![]() , where $A$
, where $A$![]() is almost simple primitive on $m$
is almost simple primitive on $m$![]() points with socle $S$
points with socle $S$![]() and $G$
and $G$![]() acts on $n=m^{r}$
acts on $n=m^{r}$![]() points (so we do not include the actions that sometimes are called holomorph compound and compound diagonal; see [Reference Liebeck, Praeger and Saxl18, Reference Praeger21] for descriptions and terminology for finite primitive permutation groups).
points (so we do not include the actions that sometimes are called holomorph compound and compound diagonal; see [Reference Liebeck, Praeger and Saxl18, Reference Praeger21] for descriptions and terminology for finite primitive permutation groups).
Proof of theorem 1.1. Assume first that the action of $G$![]() is not product action; we want to show $k(G)< n/2$
is not product action; we want to show $k(G)< n/2$![]() and $k(G)=O(n^{\delta })$
and $k(G)=O(n^{\delta })$![]() for some absolute $\delta < 1$
for some absolute $\delta < 1$![]() . We begin with the first inequality.
. We begin with the first inequality.
We have $r\geqslant 2$![]() and either $n=|S|^{r}$
and either $n=|S|^{r}$![]() , or $r=\ell t$
, or $r=\ell t$![]() with $\ell \geqslant 2$
with $\ell \geqslant 2$![]() , $t \geqslant 1$
, $t \geqslant 1$![]() and $n=|S|^{(\ell -1)t}$
and $n=|S|^{(\ell -1)t}$![]() . In particular $n \geqslant |S|^{r/2}$
. In particular $n \geqslant |S|^{r/2}$![]() . Furthermore, $G\leqslant \mathrm {Aut}(S)\wr S_r$
. Furthermore, $G\leqslant \mathrm {Aut}(S)\wr S_r$![]() . Then, by lemma 2.1 and theorem 3.5, $k(G)\leqslant k(G\cap \mathrm {Aut}(S)^{r})\cdot 2^{r-1}$
. Then, by lemma 2.1 and theorem 3.5, $k(G)\leqslant k(G\cap \mathrm {Aut}(S)^{r})\cdot 2^{r-1}$![]() . Now $G\cap \mathrm {Aut}(S)^{r}$
. Now $G\cap \mathrm {Aut}(S)^{r}$![]() admits a normal series of length $r$
admits a normal series of length $r$![]() in which every factor is almost simple with socle $S$
in which every factor is almost simple with socle $S$![]() ; therefore, by theorem 3.5, $k(G\cap \mathrm {Aut}(S)^{r})\leqslant f(S)^{r}$
; therefore, by theorem 3.5, $k(G\cap \mathrm {Aut}(S)^{r})\leqslant f(S)^{r}$![]() , where $f(S)=\text {max}\{k(A): S\leqslant A\leqslant \mathrm {Aut}(S)\}$
, where $f(S)=\text {max}\{k(A): S\leqslant A\leqslant \mathrm {Aut}(S)\}$![]() . We deduce that it is enough to show that
. We deduce that it is enough to show that
By lemma 3.1, this is true unless $S\cong A_5, A_6, \mathrm {PSL}_2(7), \mathrm {PSL}_2(11)$![]() . Assume then that we are in one of these cases. If $n=|S|^{r}$
. Assume then that we are in one of these cases. If $n=|S|^{r}$![]() or $n=|S|^{(\ell -1)t}$
or $n=|S|^{(\ell -1)t}$![]() with $\ell \geqslant 3$
with $\ell \geqslant 3$![]() , then $n\geqslant |S|^{2r/3}$
, then $n\geqslant |S|^{2r/3}$![]() , hence by the same argument as above we have $k(G)< n/2$
, hence by the same argument as above we have $k(G)< n/2$![]() provided
provided
We can check that this is true. Therefore we are reduced to the case in which $S\in \{A_5, A_6, \mathrm {PSL}_2(7), \mathrm {PSL}_2(11)\}$![]() , $r=2t$
, $r=2t$![]() and $n=|S|^{t}$
and $n=|S|^{t}$![]() .
.
Assume first that $t=1$![]() , and let $h(S)$
, and let $h(S)$![]() be the maximum number of conjugacy classes of a primitive group on $|S|$
be the maximum number of conjugacy classes of a primitive group on $|S|$![]() points with socle $S^{2}$
points with socle $S^{2}$![]() . We can use [8] in order to compute that $h(S) < |S|/2$
. We can use [8] in order to compute that $h(S) < |S|/2$![]() .
.
Next we deal with any $t\geqslant 1$![]() . We have $G\leqslant D \wr S_t$
. We have $G\leqslant D \wr S_t$![]() , where $D$
, where $D$![]() has socle $S^{2}$
has socle $S^{2}$![]() and is primitive on $|S|$
and is primitive on $|S|$![]() points. Then $k(G)\leqslant k(G\cap D^{t})\cdot 2^{t-1}$
points. Then $k(G)\leqslant k(G\cap D^{t})\cdot 2^{t-1}$![]() . Now $G\cap D^{t}$
. Now $G\cap D^{t}$![]() admits a normal series of length $t$
admits a normal series of length $t$![]() in which every factor has socle $S^{2}$
in which every factor has socle $S^{2}$![]() and is primitive on $|S|$
and is primitive on $|S|$![]() points; in particular $k(G\cap D^{t})\leqslant h(S)^{t}<(|S|/2)^{t}$
points; in particular $k(G\cap D^{t})\leqslant h(S)^{t}<(|S|/2)^{t}$![]() and therefore $k(G)<|S|^{t}/2=n/2$
and therefore $k(G)<|S|^{t}/2=n/2$![]() , as wanted.
, as wanted.
We turn now to the asymptotic statement; namely, $k(G)=O(n^{\delta })$![]() for an absolute $\delta <1$
for an absolute $\delta <1$![]() . We assume that $n$
. We assume that $n$![]() is sufficiently large and we show $k(G)\leqslant n^{\delta }$
is sufficiently large and we show $k(G)\leqslant n^{\delta }$![]() (which is equivalent up to enlarging $\delta$
(which is equivalent up to enlarging $\delta$![]() ). We will show in various places that $k(G)\leqslant n^{\delta '}$
). We will show in various places that $k(G)\leqslant n^{\delta '}$![]() for various $\delta '$
for various $\delta '$![]() . In order to simplify notation, we will always use the same symbol $\delta$
. In order to simplify notation, we will always use the same symbol $\delta$![]() —one should just take the maximum.
—one should just take the maximum.
Assume first that $S$![]() is sufficiently large. By lemma 3.1, we have $f(S) < |S|^{0.35}/2$
is sufficiently large. By lemma 3.1, we have $f(S) < |S|^{0.35}/2$![]() . Using $n \geqslant |S|^{r/2}$
. Using $n \geqslant |S|^{r/2}$![]() , we deduce $k(G)< n^{0.7}$
, we deduce $k(G)< n^{0.7}$![]() .
.
Assume now that $S$![]() has bounded order. If $S\not \cong A_5, A_6, \mathrm {PSL}_2(7), \mathrm {PSL}_2(11)$
has bounded order. If $S\not \cong A_5, A_6, \mathrm {PSL}_2(7), \mathrm {PSL}_2(11)$![]() , by lemma 3.1 we have $2f(S) < |S|^{1/2}$
, by lemma 3.1 we have $2f(S) < |S|^{1/2}$![]() , and in particular
, and in particular
for some $\delta <1$![]() absolute (since $|S|$
absolute (since $|S|$![]() is bounded).
is bounded).
Assume then that $S\cong A_5, A_6, \mathrm {PSL}_2(7), \mathrm {PSL}_2(11)$![]() . If $n=|S|^{r}$
. If $n=|S|^{r}$![]() or $n=|S|^{(\ell -1)t}$
or $n=|S|^{(\ell -1)t}$![]() with $\ell \geqslant 3$
with $\ell \geqslant 3$![]() , then $n\geqslant |S|^{2r/3}$
, then $n\geqslant |S|^{2r/3}$![]() and, as already observed, $f(S)<|S|^{2/3}/2$
and, as already observed, $f(S)<|S|^{2/3}/2$![]() ; therefore the same argument as above applies. The remaining case is $\ell =2$
; therefore the same argument as above applies. The remaining case is $\ell =2$![]() and $r=2t$
and $r=2t$![]() . We already observed that $2h(S)<|S|$
. We already observed that $2h(S)<|S|$![]() , from which we get
, from which we get
for some $\delta <1$![]() absolute.
absolute.
Assume now that the action of $G$![]() is product action, and assume that we are not in case (2) of the statement. We want to show $k(G)< n/2$
is product action, and assume that we are not in case (2) of the statement. We want to show $k(G)< n/2$![]() and $k(G)=O(n^{\delta })$
and $k(G)=O(n^{\delta })$![]() for some $\delta <1$
for some $\delta <1$![]() absolute. We begin with the first inequality. We have $G\leqslant A\wr S_r$
absolute. We begin with the first inequality. We have $G\leqslant A\wr S_r$![]() , $n=m^{r}$
, $n=m^{r}$![]() , and $A$
, and $A$![]() is an almost simple group with socle $S$
is an almost simple group with socle $S$![]() admitting a primitive action on $m$
admitting a primitive action on $m$![]() points, which is not among the possibilities of theorem 1.2(2).
points, which is not among the possibilities of theorem 1.2(2).
Note that $k(G)\leqslant k(G\cap A^{r})\cdot 2^{r-1}$![]() , and $G\cap A^{r}$
, and $G\cap A^{r}$![]() admits a normal series of length $r$
admits a normal series of length $r$![]() in which each factor is isomorphic to a subgroup $S\leqslant B\leqslant A$
in which each factor is isomorphic to a subgroup $S\leqslant B\leqslant A$![]() . By lemma 3.4, $k(B)< m/2$
. By lemma 3.4, $k(B)< m/2$![]() for every $S\leqslant B\leqslant A$
for every $S\leqslant B\leqslant A$![]() , and therefore $k(G\cap A^{r})<(m/2)^{r}$
, and therefore $k(G\cap A^{r})<(m/2)^{r}$![]() and $k(G)< n/2$
and $k(G)< n/2$![]() , as wanted.
, as wanted.
The asymptotic statement $k(G)=O(n^{\delta })$![]() for some $\delta <1$
for some $\delta <1$![]() is proved as we did for the case in which $n=|S|^{r}$
is proved as we did for the case in which $n=|S|^{r}$![]() or $n=|S|^{(\ell -1)t}$
or $n=|S|^{(\ell -1)t}$![]() , dividing the cases $|S|$
, dividing the cases $|S|$![]() sufficiently large and $|S|$
sufficiently large and $|S|$![]() bounded. If $S$
bounded. If $S$![]() is sufficiently large, by lemma 3.4 we have $k(B)< m^{0.8}/2$
is sufficiently large, by lemma 3.4 we have $k(B)< m^{0.8}/2$![]() for every $B\leqslant S\leqslant A$
for every $B\leqslant S\leqslant A$![]() , and therefore $k(G)< n^{0.8}/2$
, and therefore $k(G)< n^{0.8}/2$![]() . If $S$
. If $S$![]() has bounded order, we only need to use $k(B)< m/2$
has bounded order, we only need to use $k(B)< m/2$![]() for every $S\leqslant B\leqslant A$
for every $S\leqslant B\leqslant A$![]() , which holds again in view of lemma 3.4.
, which holds again in view of lemma 3.4.
Assume now that we are in case (2)(i) of the statement; we want to show $k(G)< n^{1.31}$![]() . We have $G\leqslant A\wr S_r$
. We have $G\leqslant A\wr S_r$![]() and $A$
and $A$![]() is almost simple acting primitively on $m$
is almost simple acting primitively on $m$![]() points.
points.
Let us consider first the case in which $A=M_{12}$![]() acting primitively on $m=12$
acting primitively on $m=12$![]() points. If $r\geqslant 4$
points. If $r\geqslant 4$![]() , [Reference Garonzi and Maróti11] tells us that a subgroup of $S_r$
, [Reference Garonzi and Maróti11] tells us that a subgroup of $S_r$![]() has at most $5^{(r-1)/3}< 5^{r/3}$
has at most $5^{(r-1)/3}< 5^{r/3}$![]() conjugacy classes. In particular, using that $k(A)= 15$
conjugacy classes. In particular, using that $k(A)= 15$![]() , we deduce that $k(G)< 15^{r} \cdot 5^{r/3}$
, we deduce that $k(G)< 15^{r} \cdot 5^{r/3}$![]() , which we verify to be at most $n^{1.31}$
, which we verify to be at most $n^{1.31}$![]() . If $r\leqslant 3$
. If $r\leqslant 3$![]() , we use that a subgroup of $S_r$
, we use that a subgroup of $S_r$![]() has at most $r$
has at most $r$![]() conjugacy classes, so $k(G)\leqslant 15^{r} \cdot r$
conjugacy classes, so $k(G)\leqslant 15^{r} \cdot r$![]() , which is less than $n^{1.31}$
, which is less than $n^{1.31}$![]() for $r\leqslant 3$
for $r\leqslant 3$![]() .
.
Let us consider now all other cases. By lemma 3.2 we have $k(B)\leqslant k(A)$![]() for every $S\leqslant B\leqslant A$
for every $S\leqslant B\leqslant A$![]() . Then $k(G)\leqslant k(A)^{r}\cdot 2^{r-1}< (2k(A))^{r}$
. Then $k(G)\leqslant k(A)^{r}\cdot 2^{r-1}< (2k(A))^{r}$![]() , so we only need to show that $2k(A)\leqslant m^{1.31}$
, so we only need to show that $2k(A)\leqslant m^{1.31}$![]() . This can be checked easily going through all cases in table 1 (but leaving out the case of $M_{12}$
. This can be checked easily going through all cases in table 1 (but leaving out the case of $M_{12}$![]() acting on $12$
acting on $12$![]() points).
points).
Assume finally that we are in case (2)(ii) of the statement, and the action of $A$![]() is isomorphic to an action in (B); in particular $m=(q^{d}-1)/(q-1)$
is isomorphic to an action in (B); in particular $m=(q^{d}-1)/(q-1)$![]() . We want to show $k(G)< n^{1.9}$
. We want to show $k(G)< n^{1.9}$![]() .
.
If $r\geqslant 4$![]() , by theorem 2.10 we have
, by theorem 2.10 we have
hence we are done provided $100\cdot 5^{1/3}\leqslant m^{0.9}$![]() , that is, $m\geqslant 303$
, that is, $m\geqslant 303$![]() . If $r\leqslant 3$
. If $r\leqslant 3$![]() , we use $k(G)\leqslant (100q^{d-1})^{r}\cdot r$
, we use $k(G)\leqslant (100q^{d-1})^{r}\cdot r$![]() , and we see that $m\geqslant 303$
, and we see that $m\geqslant 303$![]() is enough also in these cases.
is enough also in these cases.
Therefore we assume that $m<303$![]() ; this leaves us with the cases $d=6,7,8$
; this leaves us with the cases $d=6,7,8$![]() and $q=2$
and $q=2$![]() ; or $d=5$
; or $d=5$![]() and $q\leqslant 3$
and $q\leqslant 3$![]() ; or $d=4$
; or $d=4$![]() and $q\leqslant 5$
and $q\leqslant 5$![]() , or $d=3$
, or $d=3$![]() and $q\leqslant 16$
and $q\leqslant 16$![]() ; or $d=2$
; or $d=2$![]() and $q<302$
and $q<302$![]() .
.
We whittle down slightly the possibilities for $d=2$![]() . In the proof of lemma 2.12, we recalled the exact value of $k(\mathrm {PSL}_2(q))$
. In the proof of lemma 2.12, we recalled the exact value of $k(\mathrm {PSL}_2(q))$![]() and $k(\mathrm {PGL}_2(q))$
and $k(\mathrm {PGL}_2(q))$![]() . Using this and $q<302$
. Using this and $q<302$![]() , it is easy to deduce that $k(A)\leqslant 8(q+1)=8m$
, it is easy to deduce that $k(A)\leqslant 8(q+1)=8m$![]() . By the same computation as above, we are done provided $8\cdot 5^{1/3}\leqslant m^{0.9}$
. By the same computation as above, we are done provided $8\cdot 5^{1/3}\leqslant m^{0.9}$![]() , that is, $m\geqslant 19$
, that is, $m\geqslant 19$![]() . Therefore if $d=2$
. Therefore if $d=2$![]() then we may assume that $q\leqslant 17$
then we may assume that $q\leqslant 17$![]() .
.
Now we deal with all the remaining cases (for $d\leqslant 8$![]() ). We only need to show that $k(A)\cdot 5^{1/3}\leqslant m^{1.9}$
). We only need to show that $k(A)\cdot 5^{1/3}\leqslant m^{1.9}$![]() , which can be checked with [8].
, which can be checked with [8].
4. Further comments
4.1 Theorem 1.1(2)(i)
In theorem 1.1(2)(i), we proved $k(G)< n^{1.31}$![]() . Can we get better bounds? Since we have finitely many possibilities for the almost simple primitive group $A$
. Can we get better bounds? Since we have finitely many possibilities for the almost simple primitive group $A$![]() of degree $m$
of degree $m$![]() , we fix $A$
, we fix $A$![]() and $m$
and $m$![]() , and we want to estimate $k(G)$
, and we want to estimate $k(G)$![]() where $G\leqslant A\wr S_r$
where $G\leqslant A\wr S_r$![]() is primitive, mainly when $r$
is primitive, mainly when $r$![]() is large.
is large.
First, we show that it is not always true that $k(G)=o(n)$![]() as $n\rightarrow \infty$
as $n\rightarrow \infty$![]() (and in fact it is not even true that $k(G)=O(n)$
(and in fact it is not even true that $k(G)=O(n)$![]() ).
).
Lemma 4.1 Consider $A=M_{12}$![]() acting primitively on $12$
acting primitively on $12$![]() points, and consider $G=A\wr C_r$
points, and consider $G=A\wr C_r$![]() acting on $n=12^{r}$
acting on $n=12^{r}$![]() points, where $C_r$
points, where $C_r$![]() is cyclic of order $r$
is cyclic of order $r$![]() . If $r$
. If $r$![]() is large enough, then $k(G)>n^{1.08}$
is large enough, then $k(G)>n^{1.08}$![]() .
.
Proof. We have
Since $k(A)=15$![]() , this is easily seen to be larger than $n^{1.08}$
, this is easily seen to be larger than $n^{1.08}$![]() for $r$
for $r$![]() large enough.
large enough.
The same argument shows that $k(G)>n^{\alpha }$![]() for some absolute $\alpha >1$
for some absolute $\alpha >1$![]() whenever $A$
whenever $A$![]() and $m$
and $m$![]() in table 1 are such that $k(A)>m$
in table 1 are such that $k(A)>m$![]() (but in the table, $A$
(but in the table, $A$![]() and $m$
and $m$![]() are replaced by $G$
are replaced by $G$![]() and $n$
and $n$![]() ). This happens rarely; specifically, when
). This happens rarely; specifically, when
Let us consider now the case in which $k(A)\leqslant m$![]() (by looking at table 1, this is equivalent to $k(A)< m$
(by looking at table 1, this is equivalent to $k(A)< m$![]() ). By lemma 3.2, we have $k(B)\leqslant k(A)$
). By lemma 3.2, we have $k(B)\leqslant k(A)$![]() for every subgroup $S=\mathrm {Soc}(A)\leqslant B\leqslant A$
for every subgroup $S=\mathrm {Soc}(A)\leqslant B\leqslant A$![]() . We assume that $r\geqslant 4$
. We assume that $r\geqslant 4$![]() , so that by [Reference Garonzi and Maróti11] a subgroup of $S_r$
, so that by [Reference Garonzi and Maróti11] a subgroup of $S_r$![]() has at most $5^{(r-1)/3}< 5^{r/3}$
has at most $5^{(r-1)/3}< 5^{r/3}$![]() conjugacy classes. Then, we have $k(G)< (k(A)5^{1/3})^{r}$
conjugacy classes. Then, we have $k(G)< (k(A)5^{1/3})^{r}$![]() , and whenever $k(A)\cdot 5^{1/3}< m$
, and whenever $k(A)\cdot 5^{1/3}< m$![]() we get $k(G)< n^{\delta }$
we get $k(G)< n^{\delta }$![]() for some absolute $\delta <1$
for some absolute $\delta <1$![]() . The condition $k(A)\cdot 5^{1/3}< m$
. The condition $k(A)\cdot 5^{1/3}< m$![]() holds in some cases, but not quite in all.
holds in some cases, but not quite in all.
Therefore one should try to change the argument. We make the following conjecture.
Conjecture 4.2 Let $A$![]() be an almost simple primitive group on $m$
be an almost simple primitive group on $m$![]() points appearing in table 1, and assume that $k(A)< m$
points appearing in table 1, and assume that $k(A)< m$![]() . Then, for every primitive subgroup $G\leqslant A\wr S_r$
. Then, for every primitive subgroup $G\leqslant A\wr S_r$![]() on $n=m^{r}$
on $n=m^{r}$![]() points, $k(G)=o(m^{r})$
points, $k(G)=o(m^{r})$![]() as $r\rightarrow \infty$
as $r\rightarrow \infty$![]() .
.
In order to address conjecture 4.2, it seems relevant to estimate the number of conjugacy classes in wreath products (although $G$![]() need not be a full wreath product, which is a complication).
need not be a full wreath product, which is a complication).
4.2 Conjugacy classes in wreath products
Let $A\neq 1$![]() be a finite group, and let $P$
be a finite group, and let $P$![]() be a transitive permutation group of degree $r$
be a transitive permutation group of degree $r$![]() . Throughout, denote $k=k(A)$
. Throughout, denote $k=k(A)$![]() . Consider the wreath product $G=A\wr P$
. Consider the wreath product $G=A\wr P$![]() . By theorem 3.5, we have $k(G)\leqslant k^{r}\cdot 2^{r-1}$
. By theorem 3.5, we have $k(G)\leqslant k^{r}\cdot 2^{r-1}$![]() . Does a considerably better bound hold? If necessary, we may imagine that $A$
. Does a considerably better bound hold? If necessary, we may imagine that $A$![]() is fixed and $r\rightarrow \infty$
is fixed and $r\rightarrow \infty$![]() . In fact, we ask a question which is independent of the relation between $A$
. In fact, we ask a question which is independent of the relation between $A$![]() and $r$
and $r$![]() .
.
Question 2 Let $A\neq 1$![]() be a finite group, let $P\leqslant S_r$
be a finite group, let $P\leqslant S_r$![]() be transitive, and set $G=A\wr P$
be transitive, and set $G=A\wr P$![]() . Is $k(G)=O(k^{r})$
. Is $k(G)=O(k^{r})$![]() ?
?
We should note that a positive answer to question 2 would not necessarily provide a positive answer to conjecture 4.2 (since, in conjecture 4.2, $G$![]() needs not be a wreath product).
needs not be a wreath product).
The next lemma gives an affirmative answer to question 2 for the case where $P\leqslant S_r$![]() is regular. Before proving the lemma, we recall the combinatorial description of the conjugacy classes of $G=A\wr P$
is regular. Before proving the lemma, we recall the combinatorial description of the conjugacy classes of $G=A\wr P$![]() , in general: View the $k$
, in general: View the $k$![]() conjugacy classes of $A$
conjugacy classes of $A$![]() as $k$
as $k$![]() distinct colours. Let $\pi _1, \ldots, \pi _t$
distinct colours. Let $\pi _1, \ldots, \pi _t$![]() be representatives for the conjugacy classes of $P$
be representatives for the conjugacy classes of $P$![]() . For each $i$
. For each $i$![]() , colour the cycles of $\pi _i$
, colour the cycles of $\pi _i$![]() in each possible way, and identify two colourings if one is obtained from the other by conjugation in $\text {C}_P(\pi _i)$
in each possible way, and identify two colourings if one is obtained from the other by conjugation in $\text {C}_P(\pi _i)$![]() (note that $\text {C}_P(\pi _i)$
(note that $\text {C}_P(\pi _i)$![]() acts on the cycles of $\pi _i$
acts on the cycles of $\pi _i$![]() ). In this way we get the conjugacy classes of $G=A\wr P$
). In this way we get the conjugacy classes of $G=A\wr P$![]() ; these can be thought of as the conjugacy classes of $P$
; these can be thought of as the conjugacy classes of $P$![]() , in which each cycle has a colour, and two colourings are identified as described above.
, in which each cycle has a colour, and two colourings are identified as described above.
Lemma 4.3 Let $G=A\wr P$![]() with $A\neq 1$
with $A\neq 1$![]() , $P\leqslant S_r$
, $P\leqslant S_r$![]() regular, and set $k=k(A)$
regular, and set $k=k(A)$![]() . Then
. Then
Proof. Assume that $\pi \in P$![]() has order at least $2$
has order at least $2$![]() ; then $\pi$
; then $\pi$![]() has at most $r/2$
has at most $r/2$![]() cycles. Summing over all nontrivial elements $\pi \in P$
cycles. Summing over all nontrivial elements $\pi \in P$![]() , we deduce that the number of colourings of the cycles of all nontrivial elements $\pi \in P$
, we deduce that the number of colourings of the cycles of all nontrivial elements $\pi \in P$![]() is at most $rk^{r/2}$
is at most $rk^{r/2}$![]() .
.
Now we consider the colourings of the cycles of the identity element $1\in P$![]() . The action of $P=\text {C}_P(1)$
. The action of $P=\text {C}_P(1)$![]() on the cycles can clearly be identified with the action of $P$
on the cycles can clearly be identified with the action of $P$![]() on the set $\{1, \ldots, r\}$
on the set $\{1, \ldots, r\}$![]() .
.
Let $\mathcal {C}$![]() be a colouring of $\{1, \ldots, r\}$
be a colouring of $\{1, \ldots, r\}$![]() . The size of the $P$
. The size of the $P$![]() -orbit of $\mathcal {C}$
-orbit of $\mathcal {C}$![]() is strictly smaller than $r$
is strictly smaller than $r$![]() if and only if $\mathcal {C}$
if and only if $\mathcal {C}$![]() is stabilized by a nontrivial element $\pi \in P$
is stabilized by a nontrivial element $\pi \in P$![]() , which implies that $\mathcal {C}$
, which implies that $\mathcal {C}$![]() has constant colours along the cycles of $\pi$
has constant colours along the cycles of $\pi$![]() . Therefore, the number of such colourings is at most $rk^{r/2}$
. Therefore, the number of such colourings is at most $rk^{r/2}$![]() . This implies that the number of colourings whose $P$
. This implies that the number of colourings whose $P$![]() -orbit has size $r$
-orbit has size $r$![]() is at least $k^{r}-rk^{r/2}$
is at least $k^{r}-rk^{r/2}$![]() , whence
, whence
This proves the lemma.
4.3 Theorem 1.1(2)(ii)
In this case we have $G\leqslant A\wr S_r$![]() where $A$
where $A$![]() is almost simple primitive on $m$
is almost simple primitive on $m$![]() points. Work of Maróti [Reference Maróti20] tells us that $k(G)\leqslant p(n)$
points. Work of Maróti [Reference Maróti20] tells us that $k(G)\leqslant p(n)$![]() and this bound is achieved if the action of $A$
and this bound is achieved if the action of $A$![]() is isomorphic to an action in (A).
is isomorphic to an action in (A).
Assume instead that the action of $A$![]() is isomorphic to an action in (B). We have shown that, in this case, $k(G)< n^{1.9}$
is isomorphic to an action in (B). We have shown that, in this case, $k(G)< n^{1.9}$![]() . This is certainly a long way from being sharp; let us consider what might be possible.
. This is certainly a long way from being sharp; let us consider what might be possible.
First, recall that, if $q$![]() is odd, and if $A=\mathrm {PGL}_2(q)$
is odd, and if $A=\mathrm {PGL}_2(q)$![]() , then $k(A)=q+2>m=q+1$
, then $k(A)=q+2>m=q+1$![]() . If we take for instance $q=5$
. If we take for instance $q=5$![]() then, by the same argument as in lemma 4.1, we see that $k(A\wr C_r)>n^{1.08}$
then, by the same argument as in lemma 4.1, we see that $k(A\wr C_r)>n^{1.08}$![]() for $r$
for $r$![]() sufficiently large. Therefore it is not true in general that $k(G)=O(n)$
sufficiently large. Therefore it is not true in general that $k(G)=O(n)$![]() .
.
However, in the other direction, observe that, for any $G$![]() in the case under consideration, the usual bound $k(G)<(100q^{d-1})^{r} \cdot 2^{r}$
in the case under consideration, the usual bound $k(G)<(100q^{d-1})^{r} \cdot 2^{r}$![]() implies that, for every fixed $\epsilon >0$
implies that, for every fixed $\epsilon >0$![]() , $k(G)< n^{1+\epsilon }$
, $k(G)< n^{1+\epsilon }$![]() provided $\mathrm {PSL}_d(q)$
provided $\mathrm {PSL}_d(q)$![]() is sufficiently large (or, equivalently, provided $m$
is sufficiently large (or, equivalently, provided $m$![]() is sufficiently large). We are left with the natural question:
is sufficiently large). We are left with the natural question:
Question 3 Let $A$![]() be an almost simple primitive group isomorphic to a group in (B), and assume that $G\leqslant A\wr S_r$
be an almost simple primitive group isomorphic to a group in (B), and assume that $G\leqslant A\wr S_r$![]() is primitive on $n=m^{r}$
is primitive on $n=m^{r}$![]() points. What is the minimum value of $\epsilon$
points. What is the minimum value of $\epsilon$![]() such that $k(G)< n^{1+\epsilon }$
such that $k(G)< n^{1+\epsilon }$![]() ?
?