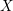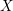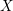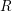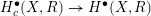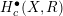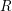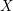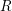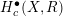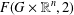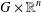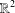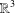Refine search
Actions for selected content:
9 results
FORBIDDEN PARTITION CONFIGURATION SPACES OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 12 February 2025, pp. 536-549
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Flat Vertex Folds: Local Properties
- from Part II - The Combinatorial Geometry of Flat Origami
-
- Book:
- Origametry
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020, pp 75-106
-
- Chapter
- Export citation
14 - Rigid Origami Theory
- from Part IV - Non-flat Folding
-
- Book:
- Origametry
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020, pp 290-318
-
- Chapter
- Export citation
13 - Rigid Foldings
- from Part IV - Non-flat Folding
-
- Book:
- Origametry
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020, pp 256-289
-
- Chapter
- Export citation
SEQUENTIAL COLLISION-FREE OPTIMAL MOTION PLANNING ALGORITHMS IN PUNCTURED EUCLIDEAN SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 506-516
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Cohomology of generalized configuration spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 251-298
- Print publication:
- February 2020
-
- Article
- Export citation
CATEGORY AND TOPOLOGICAL COMPLEXITY OF THE CONFIGURATION SPACE
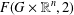 $F(G\times \mathbb{R}^{n},2)$
$F(G\times \mathbb{R}^{n},2)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 507-517
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ORBISPACES, CONFIGURATIONS AND QUASI-FIBRATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 August 2016, p. 342
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Finite type knot invariants and the calculus of functors
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 13 January 2006, pp. 222-250
- Print publication:
- January 2006
-
- Article
-
- You have access
- Export citation