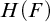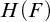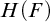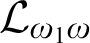Refine search
Actions for selected content:
9 results
ON EFFECTIVE CONSTRUCTIONS OF EXISTENTIALLY CLOSED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 September 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTABLE PRESENTATIONS OF C*-ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1313-1338
- Print publication:
- September 2024
-
- Article
- Export citation
INTERPRETING A FIELD IN ITS HEISENBERG GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 December 2021, pp. 1215-1230
- Print publication:
- September 2022
-
- Article
- Export citation
AN INTRODUCTION TO THE SCOTT COMPLEXITY OF COUNTABLE STRUCTURES AND A SURVEY OF RECENT RESULTS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 November 2021, pp. 71-103
- Print publication:
- March 2022
-
- Article
- Export citation
COMPUTABILITY, ORDERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1588-1598
- Print publication:
- December 2020
-
- Article
- Export citation
THE TREE OF TUPLES OF A STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 07 September 2020, pp. 21-46
- Print publication:
- March 2022
-
- Article
- Export citation
ON THE COMPLEXITY OF CLASSIFYING LEBESGUE SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1254-1288
- Print publication:
- September 2020
-
- Article
- Export citation
LEFT-ORDERABLE COMPUTABLE GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 05 February 2018, pp. 237-255
- Print publication:
- March 2018
-
- Article
- Export citation
DEGREES OF CATEGORICITY ON A CONE VIA η-SYSTEMS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 325-346
- Print publication:
- March 2017
-
- Article
- Export citation