We study competing first passage percolation on graphs generated by the configuration model with infinite-mean degrees. Initially, two uniformly chosen vertices are infected with a type 1 and type 2 infection, respectively, and the infection then spreads via nearest neighbors in the graph. The time it takes for the type 1 (resp. 2) infection to traverse an edge e is given by a random variable 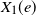 $X_1(e)$ (resp.
$X_1(e)$ (resp. 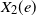 $X_2(e)$) and, if the vertex at the other end of the edge is still uninfected, it then becomes type 1 (resp. 2) infected and immune to the other type. Assuming that the degrees follow a power-law distribution with exponent
$X_2(e)$) and, if the vertex at the other end of the edge is still uninfected, it then becomes type 1 (resp. 2) infected and immune to the other type. Assuming that the degrees follow a power-law distribution with exponent 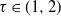 $\tau \in (1,2)$, we show that with high probability as the number of vertices tends to infinity, one of the infection types occupies all vertices except for the starting point of the other type. Moreover, both infections have a positive probability of winning regardless of the passage-time distribution. The result is also shown to hold for the erased configuration model, where self-loops are erased and multiple edges are merged, and when the degrees are conditioned to be smaller than
$\tau \in (1,2)$, we show that with high probability as the number of vertices tends to infinity, one of the infection types occupies all vertices except for the starting point of the other type. Moreover, both infections have a positive probability of winning regardless of the passage-time distribution. The result is also shown to hold for the erased configuration model, where self-loops are erased and multiple edges are merged, and when the degrees are conditioned to be smaller than 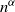 $n^\alpha$ for some
$n^\alpha$ for some 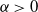 $\alpha\gt 0$.
$\alpha\gt 0$.
 ${\mathbb{Z}}$
${\mathbb{Z}}$