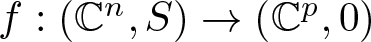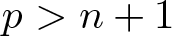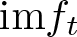Refine search
Actions for selected content:
32 results
Chapter 9 - Phonological Processes
-
- Book:
- English Phonetics and Phonology
- Published online:
- 17 October 2025
- Print publication:
- 10 July 2025, pp 122-132
-
- Chapter
- Export citation
Isotypical components of the homology of ICIS and images of deformations of map germs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-40
-
- Article
- Export citation
Chapter Eight - Genetic History of the Caucasus
-
- Book:
- The Peopling of the Caucasus
- Published online:
- 21 January 2025
- Print publication:
- 23 January 2025, pp 115-201
-
- Chapter
- Export citation
Clustering, coalescing and bursting processes in surface bubbles of surfactant water flows
-
- Journal:
- Flow: Applications of Fluid Mechanics / Volume 4 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, E17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Singularities in Action
-
- Book:
- Higher Special Functions
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 81-113
-
- Chapter
- Export citation
7 - Coalescence
- from Part IV - The Pivot
-
- Book:
- China and the Philippines
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 171-186
-
- Chapter
- Export citation
Phonology cannot transpose: evidence from Meto
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Making Community: Implications of Hybridity and Coalescence at Morton Village
-
- Journal:
- American Antiquity / Volume 88 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 01 February 2023, pp. 79-98
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 1 - Phonological Processes in Germanic Languages
- from Part I - Phonology
-
-
- Book:
- The Cambridge Handbook of Germanic Linguistics
- Published online:
- 31 March 2020
- Print publication:
- 16 April 2020, pp 11-32
-
- Chapter
- Export citation
2 - Droplets and Dispersions
-
- Book:
- Intensification of Liquid–Liquid Processes
- Published online:
- 12 May 2020
- Print publication:
- 16 April 2020, pp 43-80
-
- Chapter
- Export citation
Runoff on rooted trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1065-1085
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Two-Size Moment Multi-Fluid Model: A Robust and High-Fidelity Description of Polydisperse Moderately Dense Evaporating Sprays
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 902-943
- Print publication:
- October 2016
-
- Article
- Export citation
Coalescence on critical and subcritical multitype branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 802-817
- Print publication:
- September 2016
-
- Article
- Export citation
Perfect simulation of M/G/c queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1039-1063
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Coalescence Times for the Bienaymé-Galton-Watson Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 209-218
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
An Application of the Coalescence Theory to Branching Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 893-899
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Coalescence in Subcritical Bellman-Harris Age-Dependent Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 576-591
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Coalescence in Critical and Subcritical Galton-Watson Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 627-638
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Numerical Study of Surfactant-Laden Drop-Drop Interactions
-
- Journal:
- Communications in Computational Physics / Volume 10 / Issue 2 / August 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 453-473
- Print publication:
- August 2011
-
- Article
- Export citation
Modélisation de la propagation des fissures courtes en fatiguedans le cas du 316L
-
- Journal:
- Mechanics & Industry / Volume 11 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 24 December 2010, pp. 379-384
- Print publication:
- September 2010
-
- Article
- Export citation