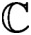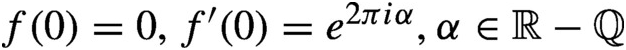Refine search
Actions for selected content:
3 results
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 3599-3629
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Loewner evolution of hedgehogs and 2-conformal measures of circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2734-2753
- Print publication:
- September 2021
-
- Article
- Export citation
AMBIGUITY IN THE DETERMINATION OF THE FREE ENERGY ASSOCIATED WITH THE CRITICAL CIRCLE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 177-184
-
- Article
-
- You have access
- Export citation