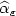Refine search
Actions for selected content:
3 results
Asymptotics for the Lp -deviation of the variance estimator under diffusion
-
- Journal:
- ESAIM: Probability and Statistics / Volume 8 / August 2004
- Published online by Cambridge University Press:
- 15 September 2004, pp. 132-149
- Print publication:
- August 2004
-
- Article
- Export citation
On the asymptotic properties of a simple estimate of the Mode
-
- Journal:
- ESAIM: Probability and Statistics / Volume 8 / August 2004
- Published online by Cambridge University Press:
- 15 September 2004, pp. 1-11
- Print publication:
- August 2004
-
- Article
- Export citation
Limit Theorems for the painting of graphs by clusters
-
- Journal:
- ESAIM: Probability and Statistics / Volume 5 / 2001
- Published online by Cambridge University Press:
- 15 August 2002, pp. 105-118
- Print publication:
- 2001
-
- Article
- Export citation