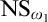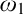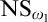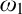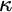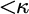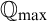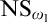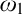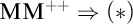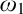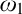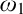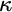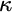Refine search
Actions for selected content:
1 results
Forcing “
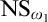 $\mathrm {NS}_{\omega _1}$ is
$\mathrm {NS}_{\omega _1}$ is 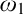 $\omega _1$-Dense” from Large Cardinals
$\omega _1$-Dense” from Large Cardinals
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, p. 544
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation