We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Consider a random vector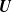 
$\textbf{U}$
whose distribution function coincides in its upper tail with that of an Archimedean copula. We report the fact that the conditional distribution of 
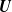$\textbf{U}$
, conditional on one of its components, has under a mild condition on the generator function independent upper tails, no matter what the unconditional tail behavior is. This finding is extended to Archimax copulas.
