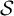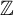Given any strong orbit equivalence class of minimal Cantor systems and any cardinal number that is finite, countable, or the continuum, we show that there exists a minimal subshift within the class whose number of asymptotic components is exactly the given cardinal. For finite or countable ones, we explicitly construct such examples using 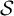$\mathcal {S}$-adic subshifts. We obtain the uncountable case by showing that any topological dynamical system with at most countably many asymptotic components has zero topological entropy. We also construct systems that have arbitrarily high subexponential word complexity, but only one asymptotic component. We deduce that within any strong orbit equivalence class, there exists a minimal subshift whose automorphism group is isomorphic to 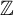$\mathbb {Z}$.

Two asymptotic configurations on a full $\mathbb {Z}^d$-shift are indistinguishable if, for every finite pattern, the associated sets of occurrences in each configuration coincide up to a finitely supported permutation of $\mathbb {Z}^d$. We prove that indistinguishable asymptotic pairs satisfying a ‘flip condition’ are characterized by their pattern complexity on finite connected supports. Furthermore, we prove that uniformly recurrent indistinguishable asymptotic pairs satisfying the flip condition are described by codimension-one (dimension of the internal space) cut and project schemes, which symbolically correspond to multidimensional Sturmian configurations. Together, the two results provide a generalization to $\mathbb {Z}^d$ of the characterization of Sturmian sequences by their factor complexity $n+1$. Many open questions are raised by the current work and are listed in the introduction.