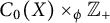Refine search
Actions for selected content:
1 results
Ideals with approximate unit in semicrossed products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 September 2023, pp. 257-264
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation