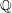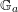Refine search
Actions for selected content:
2 results
FANO FOURFOLDS WITH LARGE ANTICANONICAL BASE LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1021-1051
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cylinders in singular del Pezzo surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 21 April 2016, pp. 1198-1224
- Print publication:
- June 2016
-
- Article
- Export citation