Refine search
Actions for selected content:
1 results
Topologizing Different Classes of Real Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 6 / 01 December 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1188-1207
- Print publication:
- 01 December 1994
-
- Article
-
- You have access
- Export citation
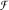 of functions from
of functions from 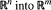 can be topologized in a sense that there exist topologies τ
can be topologized in a sense that there exist topologies τ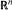 and
and 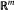 respectively, such that
respectively, such that 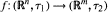 . We will show that the Generalized Continuum Hypothesis GCH implies the positive answer for this question for a large number of classes of functions
. We will show that the Generalized Continuum Hypothesis GCH implies the positive answer for this question for a large number of classes of functions  such that the class L of all linear functions g(x) = ax + b coincides with
such that the class L of all linear functions g(x) = ax + b coincides with 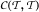 . This gives an affirmative answer to a question of Sam Nadler. The above corollary remains true for the class
. This gives an affirmative answer to a question of Sam Nadler. The above corollary remains true for the class  of all polynomials, the class
of all polynomials, the class  of all analytic functions and the class of all harmonic functions.
of all analytic functions and the class of all harmonic functions.