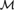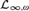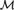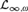Refine search
Actions for selected content:
2 results
2 - The Iterative Conception
-
- Book:
- Conceptions of Set and the Foundations of Mathematics
- Published online:
- 09 January 2020
- Print publication:
- 23 January 2020, pp 36-69
-
- Chapter
- Export citation
ZFC PROVES THAT THE CLASS OF ORDINALS IS NOT WEAKLY COMPACT FOR DEFINABLE CLASSES
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 May 2018, pp. 146-164
- Print publication:
- March 2018
-
- Article
- Export citation