Refine search
Actions for selected content:
52 results
5 - Empirical Assessment of Sequential-Sampling Models
-
- Book:
- Diffusion Process Models of Decision Making
- Published online:
- 26 October 2025
- Print publication:
- 13 November 2025, pp 92-116
-
- Chapter
- Export citation
11 - Neural Diffusion Models, II. Poisson Shot Noise and Related Models
-
- Book:
- Diffusion Process Models of Decision Making
- Published online:
- 26 October 2025
- Print publication:
- 13 November 2025, pp 287-342
-
- Chapter
- Export citation
2 - Preliminaries
-
- Book:
- Large-Scale System Analysis Under Uncertainty
- Published online:
- 17 January 2022
- Print publication:
- 17 February 2022, pp 16-53
-
- Chapter
- Export citation
6 - Continuous-Time Systems: Probabilistic Input Uncertainty
-
- Book:
- Large-Scale System Analysis Under Uncertainty
- Published online:
- 17 January 2022
- Print publication:
- 17 February 2022, pp 166-201
-
- Chapter
- Export citation
Assouad Dimension of Random Processes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 281-290
-
- Article
- Export citation
On the Backward Euler Approximation of the Stochastic Allen-Cahn Equation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 323-338
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
On Durbin's Series for the Density of First Passage Times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-722
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
An approximation for the inverse first passage time problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 264-275
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Random fractals generated by a local Gaussian process indexed by a class of functions
-
- Journal:
- ESAIM: Probability and Statistics / Volume 15 / 2011
- Published online by Cambridge University Press:
- 05 January 2012, pp. 249-269
- Print publication:
- 2011
-
- Article
- Export citation
Optimization under the P M λ,τ policy of a finite dam with both continuous and jumpwise inputs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 587-594
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Ruin Probabilities for Two Classes of Risk Processes
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 35 / Issue 1 / May 2005
- Published online by Cambridge University Press:
- 17 April 2015, pp. 61-77
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
Explicit Bounds for Approximation Rates of Boundary Crossing Probabilities for the Wiener Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 82-92
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Total duration of negative surplus for the compound Poisson process that is perturbed by diffusion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 517-532
- Print publication:
- September 2002
-
- Article
- Export citation
Boundary crossing probability for Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 152-164
- Print publication:
- March 2001
-
- Article
- Export citation
The ruin problem and cover times of asymmetric random walks and Brownian motions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 177-192
- Print publication:
- March 2000
-
- Article
- Export citation
The final size of a nearly critical epidemic, and the first passage time of a Wiener process to a parabolic barrier
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 671-682
- Print publication:
- September 1998
-
- Article
- Export citation
Diffusion Approximation for Random Walks on Anisotropic Lattices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 206-212
- Print publication:
- March 1998
-
- Article
- Export citation
Boundary crossing probability for Brownian motion and general boundaries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 54-65
- Print publication:
- March 1997
-
- Article
- Export citation
First passage time distribution of a Wiener process with drift concerning two elastic barriers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 164-175
- Print publication:
- March 1996
-
- Article
- Export citation
Two Stochastic Approaches for Discounting Actuarial Functions
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 24 / Issue 2 / November 1994
- Published online by Cambridge University Press:
- 29 August 2014, pp. 167-181
- Print publication:
- November 1994
-
- Article
-
- You have access
- Export citation
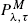 policy, where the input of water is formed by a Wiener process subject to random jumps arriving according to a Poisson process. The long-run average cost per unit time is obtained after assigning costs to the changes of release rate, a reward to each unit of output, and a penalty that is a function of the level of water in the reservoir.
policy, where the input of water is formed by a Wiener process subject to random jumps arriving according to a Poisson process. The long-run average cost per unit time is obtained after assigning costs to the changes of release rate, a reward to each unit of output, and a penalty that is a function of the level of water in the reservoir.