In this note we give simple proofs of several results involving maximal truncated Calderón–Zygmund operators in the general setting of rearrangement-invariant quasi-Banach function spaces by sparse domination. Our techniques allow us to track the dependence of the constants in weighted norm inequalities; additionally, our results hold in ℝn as well as in many spaces of homogeneous type.

Mixed norm inequalities for directional operators are closely related to the boundedness problems of several important operators in harmonic analysis. In this paper we prove weighted inequalities for some one-dimensional one-sided maximal functions. Then by applying these results, we establish mixed norm inequalities for directional maximal operators which are defined from these one-dimensional maximal functions. We also estimate the constants in these inequalities.

We prove optimal radially weighted L2-norm inequalities for the Fourier extension operator associated to the unit sphere in ℝn. Such inequalities valid at all scales are well understood. The purpose of this short paper is to establish certain more delicate single-scale versions of these.

We present “reiteration theorems” with limiting values $\theta =0$ and $\theta =1$ for a real interpolation method involving broken-logarithmic functors. The resulting spaces lie outside of the original scale of spaces and to describe them new interpolation functors are introduced. For an ordered couple of (quasi-) Banach spaces similar results were presented without proofs by Doktorskii in $[\text{D}]$.

In this paper we characterize weighted Lorentz norm inequalities for the one sided Hardy-Littlewood maximal function

Similar questions are discussed for the maximal operator associated to an invertible measure preserving transformation of a measure space.

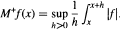
The good weights for the one-sided Hardy-Littlewood operators have been characterized by conditions . In this paper we introduce a new condition which is analogous to A∞. We show several characterizations of . For example, we prove that the class of weights is the union of classes. We also give a new characterization of weights. Finally, as an application of condition, we characterize the weights for one-sided fractional integrals and one-sided fractional maximal operators.

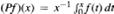The purpose of this paper is to characterize the weight functions for which the Hardy operator , with non-decreasing function ƒ, is bounded between various weighted Lp-spaces for a wide range of indices. Our characterizations complement for the most part those of E. T. Sawyer [11] and V. D. Stepanov [15] for the Hardy operator of non-increasing function.

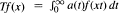The nonnegative weight function pairs u, v for which the operator maps the nonnegative nonincreasing functions in LP(v) boundedly into weak Lq(u) are characterized. This result is used, in particular, both to generalize and to provide an alternate proof of certain strong type inequalities recently obtained by Ariño and Muckenhouptfor the Hardy averaging operator restricted to nonnegative nonincreasing functions.