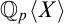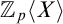When is an ideal of a ring radical or prime? By examining its generators, one may in many cases definably and uniformly test the ideal’s properties. We seek to establish such definable formulas in rings of p-adic power series, such as 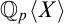 $\mathbb Q_{p}\langle X\rangle $,
$\mathbb Q_{p}\langle X\rangle $, 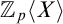 $\mathbb Z_{p}\langle X\rangle $, and related rings of power series over more general valuation rings and their fraction fields. We obtain a definable, uniform test for radicality, and, in the one-dimensional case, for primality. This builds upon the techniques stemming from the proof of the quantifier elimination results for the analytic theory of the p-adic integers by Denef and van den Dries, and the linear algebra methods of Hermann and Seidenberg.
$\mathbb Z_{p}\langle X\rangle $, and related rings of power series over more general valuation rings and their fraction fields. We obtain a definable, uniform test for radicality, and, in the one-dimensional case, for primality. This builds upon the techniques stemming from the proof of the quantifier elimination results for the analytic theory of the p-adic integers by Denef and van den Dries, and the linear algebra methods of Hermann and Seidenberg.
Abstract prepared by Madeline G. Barnicle.
E-mail: barnicle@math.ucla.edu
URL: https://escholarship.org/uc/item/6t02q9s4