The Association for Symbolic Logic publishes abstracts of recent PhD theses in logic. The aim of this activity is to publish abstracts for the majority of recent PhD theses in logic world wide and submitted abstracts will therefore only be edited to ensure that they fall within the general area of logic and are appropriate in terms of length and content. This section will provide a permanent publicly accessible overview of theses in logic and thus make up for the lack of central repository for the theses themselves. The Thesis Abstracts Section is edited by Christian Rosendal. Any abstract should formally be submitted by the thesis advisor though it is expected to usually be prepared by the candidate. For detailed instructions for preparation and submission, including the required TeX template, please consult the link below. http://aslonline.org/LogicThesisAbstracts.html
Uniform Properties of Ideals in Rings of Restricted Power Series
Published online by Cambridge University Press: 28 June 2022
Abstract
When is an ideal of a ring radical or prime? By examining its generators, one may in many cases definably and uniformly test the ideal’s properties. We seek to establish such definable formulas in rings of p-adic power series, such as 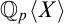 $\mathbb Q_{p}\langle X\rangle $,
$\mathbb Q_{p}\langle X\rangle $, 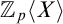 $\mathbb Z_{p}\langle X\rangle $, and related rings of power series over more general valuation rings and their fraction fields. We obtain a definable, uniform test for radicality, and, in the one-dimensional case, for primality. This builds upon the techniques stemming from the proof of the quantifier elimination results for the analytic theory of the p-adic integers by Denef and van den Dries, and the linear algebra methods of Hermann and Seidenberg.
$\mathbb Z_{p}\langle X\rangle $, and related rings of power series over more general valuation rings and their fraction fields. We obtain a definable, uniform test for radicality, and, in the one-dimensional case, for primality. This builds upon the techniques stemming from the proof of the quantifier elimination results for the analytic theory of the p-adic integers by Denef and van den Dries, and the linear algebra methods of Hermann and Seidenberg.
Abstract prepared by Madeline G. Barnicle.
E-mail: barnicle@math.ucla.edu
MSC classification
Information
- Type
- Thesis Abstracts
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
Footnotes
Supervised by Matthias Aschenbrenner.
- 1
- Cited by


