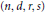Refine search
Actions for selected content:
6 results
Apolar Schemes of Algebraic Forms
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 3 / 01 June 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 476-491
- Print publication:
- 01 June 2006
-
- Article
-
- You have access
- Export citation
Additive representation in short intervals, I: Waring's problem for cubes
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1197-1220
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation
A light-weight version of Waring's problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-316
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
SLIM EXCEPTIONAL SETS FOR SUMS OF FOUR SQUARES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 85 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 09 July 2002, pp. 1-21
- Print publication:
- March 2002
-
- Article
- Export citation
ON WARING'S PROBLEM FOR CUBES AND SMOOTH WEYL SUMS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 82 / Issue 1 / January 2001
- Published online by Cambridge University Press:
- 12 January 2001, pp. 89-109
- Print publication:
- January 2001
-
- Article
- Export citation
On the Representations of a Number as the Sum of Three Cubes and a Fourth or Fifth Power
-
- Journal:
- Compositio Mathematica / Volume 121 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 55-78
- Print publication:
- March 2000
-
- Article
-
- You have access
- Export citation