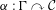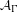Refine search
Actions for selected content:
4 results
On compact uniformly recurrent subgroups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 October 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuum of allosteric actions for non-amenable surface groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1581-1596
- Print publication:
- June 2024
-
- Article
- Export citation
Free minimal actions of countable groups with invariant probability measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1369-1389
- Print publication:
- May 2021
-
- Article
- Export citation
Amenable uniformly recurrent subgroups and lattice embeddings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1464-1501
- Print publication:
- May 2021
-
- Article
- Export citation