Refine search
Actions for selected content:
2 results
A
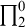 $ \prod _{2}^{0}$ SINGLETON OF MINIMAL ARITHMETIC DEGREE
$ \prod _{2}^{0}$ SINGLETON OF MINIMAL ARITHMETIC DEGREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Definability in the local structure of the ω-Turing degrees
-
- Journal:
- Mathematical Structures in Computer Science / Volume 29 / Issue 7 / August 2019
- Published online by Cambridge University Press:
- 21 February 2019, pp. 927-937
-
- Article
- Export citation