Let F be a real number field with r1 real embeddings. In this paper, we prove that the sequence
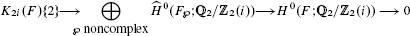
is a complex, where 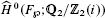 are the Tate cohomology groups. Moreover if i ≡ 0, 1, or 2 (mod 4), then it is exact; if i ≡ 3 (mod 4), then the homology group at the second term of this complex is isomorphic to
are the Tate cohomology groups. Moreover if i ≡ 0, 1, or 2 (mod 4), then it is exact; if i ≡ 3 (mod 4), then the homology group at the second term of this complex is isomorphic to 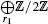 .
.