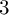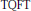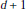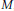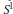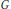We study the behaviour of Kauffman bracket skein modules of 3-manifolds under gluing along surfaces. For this we extend this notion to 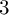 $3$-manifolds with marking consisting of open intervals and circles in the boundary. The new module is called the stated skein module.
$3$-manifolds with marking consisting of open intervals and circles in the boundary. The new module is called the stated skein module.
The first results concern non-injectivity of certain natural maps defined when forming connected sums along spheres or disks. These maps are injective for surfaces or for generic quantum parameter, but we show that in general they are not when the quantum parameter is a root of 1. We show that when the quantum parameter is a root of 1, the empty skein is zero in a connected sum where each constituent manifold has non-empty marking. We also prove various non-injectivity results for the Chebyshev-Frobenius map and the map induced by deleting marked balls.
We then interpret stated skein modules as a monoidal symmetric functor from a category of “decorated cobordisms” to a category of algebras and their bimodules. We apply this to deduce properties of stated skein modules as a Van-Kampen like theorem, a computation through Heegaard decompositions and a relation to Hochshild homology for trivial circle bundles over surfaces.