Refine search
Actions for selected content:
3 results
CONGRUENCE OF ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 746-761
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Projective Cover of an orbit space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-312
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
The Maximal Extension of a Zero-dimensional Product Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 2 / 01 June 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 192-201
- Print publication:
- 01 June 1983
-
- Article
-
- You have access
- Export citation
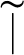
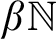
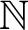
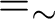
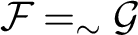
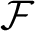
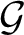
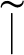
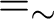
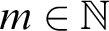
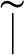
 of Tychonoff spaces is closed-hereditary, productive and possessed by all compact Hausdorff spaces, then each (0-dimensional) Tychonoff space X is a dense subspace of a (0-dimensional) Tychonoff space
of Tychonoff spaces is closed-hereditary, productive and possessed by all compact Hausdorff spaces, then each (0-dimensional) Tychonoff space X is a dense subspace of a (0-dimensional) Tychonoff space  with
with  if and only if
if and only if  , then
, then 