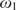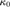Refine search
Actions for selected content:
2 results
ON
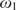 ${\omega _1}$-STRONGLY COMPACT CARDINALS
${\omega _1}$-STRONGLY COMPACT CARDINALS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 266-278
- Print publication:
- March 2014
-
- Article
- Export citation
A power function with a fixed finite gap everywhere
-
- Journal:
- The Journal of Symbolic Logic / Volume 72 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 12 March 2014, pp. 361-417
- Print publication:
- June 2007
-
- Article
- Export citation