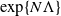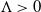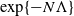Refine search
Actions for selected content:
43 results
Optimizing radiation patterns of mechanically reconfigurable phased arrays using flexible meta-gaps
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 16 / Issue 5 / June 2024
- Published online by Cambridge University Press:
- 02 January 2025, pp. 838-851
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Simulated Annealing Methodology for Clusterwise Linear Regression
-
- Journal:
- Psychometrika / Volume 54 / Issue 4 / December 1989
- Published online by Cambridge University Press:
- 01 January 2025, pp. 707-736
-
- Article
- Export citation
CLASSI: A classification model for the study of sequential processes and individual differences therein
-
- Journal:
- Psychometrika / Volume 73 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 January 2025, pp. 107-124
-
- Article
- Export citation
The Local Minima Problem in Hierarchical Classes Analysis: An Evaluation of a Simulated Annealing Algorithm and Various Multistart Procedures
-
- Journal:
- Psychometrika / Volume 72 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 January 2025, pp. 377-391
-
- Article
- Export citation
A Latent Class Multidimensional Scaling Model for Two-Way One-Mode Continuous Rating Dissimilarity Data
-
- Journal:
- Psychometrika / Volume 74 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 January 2025, pp. 297-315
-
- Article
- Export citation
Analysis of the Weighted Kappa and Its Maximum with Markov Moves
-
- Journal:
- Psychometrika / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1270-1289
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exemplar-Based Clustering via Simulated Annealing
-
- Journal:
- Psychometrika / Volume 74 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 January 2025, pp. 457-475
-
- Article
- Export citation
Clustering Qualitative Data Based on Binary Equivalence Relations: Neighborhood Search Heuristics for the Clique Partitioning Problem
-
- Journal:
- Psychometrika / Volume 74 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 January 2025, pp. 685-703
-
- Article
- Export citation
15 - Group Problem Solving: Harnessing the Wisdom of the Crowds
- from Part IV - Society
-
- Book:
- Behavioral Network Science
- Published online:
- 08 November 2024
- Print publication:
- 19 December 2024, pp 244-257
-
- Chapter
- Export citation
5 - Multivariate Feature Selection
- from Part I - Framework for Multivariate Biomarker Discovery
-
- Book:
- Multivariate Biomarker Discovery
- Published online:
- 30 May 2024
- Print publication:
- 06 June 2024, pp 76-98
-
- Chapter
- Export citation
Improved Metropolis–Hastings algorithms via landscape modification with applications to simulated annealing and the Curie–Weiss model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 587-620
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 85-125
- Print publication:
- March 2023
-
- Article
- Export citation
Aircraft sequencing and scheduling in TMAs under wind direction uncertainties
-
- Journal:
- The Aeronautical Journal / Volume 124 / Issue 1282 / December 2020
- Published online by Cambridge University Press:
- 13 August 2020, pp. 1896-1912
-
- Article
- Export citation
Predicting the flowering date of Portuguese grapevine varieties using temperature-based phenological models: a multi-site approach
-
- Journal:
- The Journal of Agricultural Science / Volume 156 / Issue 7 / September 2018
- Published online by Cambridge University Press:
- 24 October 2018, pp. 865-876
-
- Article
- Export citation
Automated statistical matching of multiple tephra records exemplified using five long maar sequences younger than 75 ka, Auckland, New Zealand
-
- Journal:
- Quaternary Research / Volume 82 / Issue 2 / September 2014
- Published online by Cambridge University Press:
- 20 January 2017, pp. 405-419
-
- Article
- Export citation
Designing efficient sampling schemes for reconnaissance surveys of contaminated bed sediments in water courses
-
- Journal:
- Netherlands Journal of Geosciences / Volume 79 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 April 2016, pp. 441-447
-
- Article
-
- You have access
- Export citation
Means in complete manifolds: uniqueness and approximation
-
- Journal:
- ESAIM: Probability and Statistics / Volume 18 / 2014
- Published online by Cambridge University Press:
- 27 March 2014, pp. 185-206
- Print publication:
- 2014
-
- Article
- Export citation