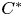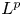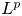Refine search
Actions for selected content:
54 results
6 - The Divine Nature
- from Part II - Theological Themes
-
-
- Book:
- The Origins of Scholasticism
- Published online:
- 18 November 2025
- Print publication:
- 08 January 2026, pp 183-207
-
- Chapter
- Export citation
Chapter 3 - Theories, Models, and Methods
-
- Book:
- Entanglements in World Politics
- Published online:
- 27 November 2025
- Print publication:
- 11 December 2025, pp 103-132
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Chapter 4 - Singular Compositional Abduction
-
- Book:
- Compositional Abduction and Scientific Interpretation
- Published online:
- 20 November 2025
- Print publication:
- 04 December 2025, pp 82-115
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
On the Use of Parsimony in Archaeological Reasoning
-
- Journal:
- American Antiquity , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Simplexity
-
- Book:
- Automated Agencies
- Published online:
- 03 April 2025
- Print publication:
- 10 April 2025, pp 57-70
-
- Chapter
- Export citation
The relevance of irrelevant information
-
- Journal:
- Experimental Economics / Volume 24 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 March 2025, pp. 985-1018
-
- Article
- Export citation
Transforming Three-Way Arrays to Maximal Simplicity
-
- Journal:
- Psychometrika / Volume 67 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 January 2025, pp. 351-365
-
- Article
- Export citation
Simplicity of non-associative skew Laurent polynomial rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
11 - Constructing words
- from Part II - Constructions and meanings
-
- Book:
- First Language Acquisition
- Published online:
- 01 November 2024
- Print publication:
- 20 June 2024, pp 311-338
-
- Chapter
- Export citation
A Compelling Conclusion (Hopefully)
-
- Book:
- Compelling Communication
- Published online:
- 30 May 2024
- Print publication:
- 30 May 2024, pp 319-324
-
- Chapter
- Export citation

Laws of Physics
-
- Published online:
- 22 May 2024
- Print publication:
- 20 June 2024
-
- Element
- Export citation
Topologically free actions and ideals in twisted Banach algebra crossed products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-31
-
- Article
- Export citation
Trinity, simplicity, and contradictory theology: a theologian's reflections
-
- Journal:
- Religious Studies / Volume 60 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 699-705
- Print publication:
- December 2024
-
- Article
- Export citation
Glutty and simple?
-
- Journal:
- Religious Studies / Volume 60 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 14 March 2024, pp. 695-698
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIVIDING LINES BETWEEN POSITIVE THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 December 2023, pp. 1-25
-
- Article
- Export citation
Chapter 25 - The Simplicity of Messiaen
- from Part IV - Concepts and Legacy
-
-
- Book:
- Messiaen in Context
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 233-239
-
- Chapter
- Export citation
3 - Simplicity and Power
-
- Book:
- Knowledge, Faith, and Early Christian Initiation
- Published online:
- 11 October 2023
- Print publication:
- 19 October 2023, pp 69-92
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
‘Orthodox panentheism’ is neither orthodox nor coherent
-
- Journal:
- Religious Studies / Volume 61 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 October 2023, pp. 427-439
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Introducing Derrida
-
- Article
- Export citation
Necessary existent theology
-
- Journal:
- Religious Studies / Volume 60 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 March 2023, pp. 204-218
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation