Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-31T03:31:18.845Z Has data issue: false hasContentIssue false
  • English
  • Français

Topologically free actions and ideals in twisted Banach algebra crossed products

Part of: Connections with other structures, applications Rings and algebras arising under various constructions Linear spaces and algebras of operators

Published online by Cambridge University Press:  26 April 2024

Krzysztof Bardadyn Open the ORCID record for Krzysztof Bardadyn [Opens in a new window]  and
Bartosz Kwaśniewski Open the ORCID record for Bartosz Kwaśniewski [Opens in a new window]
Krzysztof Bardadyn
Affiliation:
Faculty of Mathematics, University of Białystok, ul. K. Ciołkowskiego 1M, 15-245 Białystok, Poland (k.bardadyn@uwb.edu.pl;b.kwasniewski@uwb.edu.pl)
Bartosz Kwaśniewski
Affiliation:
Faculty of Mathematics, University of Białystok, ul. K. Ciołkowskiego 1M, 15-245 Białystok, Poland (k.bardadyn@uwb.edu.pl;b.kwasniewski@uwb.edu.pl)
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize the influential $C^*$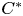-algebraic results of Kawamura–Tomiyama and Archbold–Spielberg for crossed products of discrete groups actions to the realm of Banach algebras and twisted actions. We prove that topological freeness is equivalent to the intersection property for all reduced twisted Banach algebra crossed products coming from subgroups, and in the untwisted case to a generalized intersection property for a full $L^p$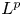-operator algebra crossed product for any $p\in [1,\,\infty ]$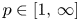. This gives efficient simplicity criteria for various Banach algebra crossed products. We also use it to identify the prime ideal space of some crossed products as the quasi-orbit space of the action. For amenable actions we prove that the full and reduced twisted $L^p$-operator algebras coincide.

Keywords

crossed producttopological freenesssimplicity

MSC classification

Primary: 47L10: Algebras of operators on Banach spaces and other topological linear spaces
Secondary: 16S35: Twisted and skew group rings, crossed products 54H15: Transformation groups and semigroups

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 31
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anantharaman-Delaroche, C.. Amenability and exactness for dynamical systems and their $C^*$-algebras. Trans. Amer. Math. Soc. 354 (2002), 4153–4178.CrossRefGoogle Scholar
Antonevich, A. and Lebedev, A.. Functional differential equations: I. $C^*$-theory, Longman Scientific & Technical, Pitman Monographs and Surveys in Pure and Applied Mathematics Vol. 70 (1994).Google Scholar
Austad, A. and Ortega, E.. Groupoids and Hermitian Banach *-algebras. Int. J. Math. 33 (2022), 2250090.CrossRefGoogle Scholar
Archbold, R. J. and Spielberg, J. S.. Topologically free actions and ideals in discrete $C^*$-dynamical systems. Proc. Einburgh Math. Soc. (2) 37 (1993), 119–124.CrossRefGoogle Scholar
Bardadyn, K. and Kwaśniewski, B. K.. Spectrum of weighted isometries: $C^*$-algebras, transfer operators and topological pressure. Isr. J. Math. 246 (2021), 149–210.CrossRefGoogle Scholar
Bardadyn, K., Kwaśniewski, B. and Mckee, A.. Banach algebras associated to twisted étale groupoids: inverse semigroup disintegration and representations on $L^p$-spaces, preprint Arxiv:2303.09997.Google Scholar
Boedihardjo, M.. $C^*$-algebras isomorphically representable on $\ell ^p$. Anal. PDE 13 (2020), 2173–2181.CrossRefGoogle Scholar
Bonsall, F. F.. A minimal property of the norm in some Banach algebras. J. London Math. Soc. 29 (1954), 156–164.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N.. $C^*$-Algebras and Finite-dimensional Approximations, Graduate Studies in Mathematics, Vol. 88 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Busby, R. C. and Smith, H. A.. Representations of twisted group algebras. Trans. Amer. Math. Soc. 149 (1970), 503–537.CrossRefGoogle Scholar
Buss, A., Echterhoff, S. and Willett, R.. Exotic crossed products and the Baum-Connes conjecture. J. Reine Angew. Math. 740 (2018), 111–159.CrossRefGoogle Scholar
Choi, Y., Gardella, E. and Thiel, H.. Rigidity results for $L^p$-operator algebras and applications, preprint Arxiv:math.OA/1909.03612, 2019.Google Scholar
Chung, Y. C.. Dynamical complexity and $K$-theory of $L^p$ operator crossed products. J. Topol. Anal. 13 (2021), 809–841.CrossRefGoogle Scholar
Dirksen, S., de Jeu, M. and Wortel, M.. Crossed products of Banach algebras. I, preprint arXiv:1104.5151v2.Google Scholar
Effros, E. G. and Hahn, F.. Locally compact transformation groups and $C^*$-algebras. Mem. Amer. Math. Soc. no. 75 (1967), 92.Google Scholar
Exel, R.. Partial dynamical systems, Fell bundles and applications, Mathematical Surveys and Monographs, Vol. 224 (AMS, 2017).CrossRefGoogle Scholar
Exel, R., Laca, M. and Quigg, John. Partial dynamical systems and $C^*$-algebras generated by partial isometries. J. Operator Theory 47 (2002), 169–186.Google Scholar
Fell, J. M. G. and Doran, R. S.. Representations of *-algebras, locally compact groups, and Banach *-algebraic bundles, Pure and Applied Mathematics, Vol. 125 (Academic Press, 1988).Google Scholar
Gardella, E.. A modern look at algebras of operators on $L^p$-spaces. Expo. Math. 39 (2021), 420–453.CrossRefGoogle Scholar
Gardella, E. and Lupini, M.. Representations of étale groupoids on $L^p$-spaces. Adv. Math. 318 (2017), 233–278.CrossRefGoogle Scholar
Gardella, E. and Thiel, H.. Quotients of Banach algebras acting on $L^p$-spaces. Adv. Math. 296 (2016), 85–92.CrossRefGoogle Scholar
Gardella, E. and Thiel, H.. Representations of $p$-convolution algebras on $L^q$-spaces. Trans. Amer. Math. Soc 371 (2019), 2207–2236.CrossRefGoogle Scholar
Gardella, E. and Thiel, H.. Isomorphisms of algebras of convolution operators. Ann. Sci. École Nor. Sup. (4) 55 (2022), 1433–1471.CrossRefGoogle Scholar
Green, P.. The local structure of twisted covariance algebras. Acta Math. 140 (1978), 191–250.CrossRefGoogle Scholar
Hejazian, S. and Pooya, S.. Simple reduced $L^p$-operator crossed products with unique trace. J. Operator Theory 74 (2015), 133–147.CrossRefGoogle Scholar
Hetland, E. V. and Ortega, E.. Rigidity of twisted groupoid $L^p$-operator algebras. J. Funct. Anal 285 (2023), 110037.CrossRefGoogle Scholar
Kawamura, S. and Tomiyama, J.. Properties of topological dynamical systems and corresponding $C^*$-algebras. Tokyo J. Math. 13 (1990), 251–257.CrossRefGoogle Scholar
Kwaśniewski, B. K. and Meyer, R.. Aperiodicity, topological freeness and pure outerness: from group actions to Fell bundles. Studia Math. 241 (2018), 257–303.CrossRefGoogle Scholar
Kwaśniewski, B. K. and Meyer, R.. Stone duality and quasi-orbit spaces for generalised $C^*$- inclusions. Proc. Lond. Math. Soc. (3) 121 (2020), 788–827.CrossRefGoogle Scholar
Kwaśniewski, B. K. and Meyer, R.. Essential crossed products by inverse semigroup actions: simplicity and pure infiniteness. Doc. Math. 26 (2021), 271–335.CrossRefGoogle Scholar
Kwaśniewski, B. K. and Meyer, R.. Aperiodicity: the almost extension property and uniqueness of pseudo-expectations. IMRN 2022 (2022), 14384–14426.CrossRefGoogle Scholar
Liao, B. and Yu, G., K-theory of group Banach algebras and Banach property RD, preprint arXiv: 1708.01982v2 [math.FA].Google Scholar
O'Donovan, D. P.. Weighted shifts and covariance algebras. Trans. Amer. Math. Soc. 208 (1975), 1–25.CrossRefGoogle Scholar
Olesen, D. and Pedersen, G. K.. Applications of the Connes spectrum to $C^*$-dynamical systems. III. J. Funct. Anal. 45 (1982), 357–390.CrossRefGoogle Scholar
Packer, J. A. and Raeburn, I.. Twisted crossed products of $C^*$-algebras. Math. Proc. Camb. Soc. 106 (1989), 0–0.Google Scholar
Phillips, N. C.. Crossed products of $L^p$ operator algebras and the $K$-theory of Cuntz algebras on $L^p$ spaces, preprint arXiv:1309.6406, 2013, p. 54.Google Scholar
Phillips, N. C.. Simplicity of reduced group Banach algebras, preprint arXiv:1909.11278, 2019, p. 25.Google Scholar
Renault, J.. The ideal structure of groupoid crossed product $C^*$-algebras. J. Operator Theory 25 (1991), 3–36.Google Scholar
Rørdam, M.. Irreducible inclusions of simple $C^*$-algebras. Enseign. Math. 69 (2023), 275–314.CrossRefGoogle Scholar
Sierakowski, A.. The ideal structure of reduced crossed products. Münster J. Math. 3 (2010), 237–261.Google Scholar
Tomiyama, J.. The Interplay Between Topological Dynamics and Theory of $C^*$-Algebras, Lecture Notes Ser., Vol. 2 (Res. Inst. Math., Seoul, 1992).Google Scholar
Wang, Z. and Zhu, S.. On the Takai duality for $L^p$ operator crossed products, preprint arXiv:2212.00408.Google Scholar
Zeller-Meier, G.. Produits croises d'une $C^*$-algebre par un groupe d'automorphismes. J. Math. Pures Appl. 47 (1968), 101–239.Google Scholar