We consider the algebraic group GL1 (A), where A is a division algebra of prime degree over a field F, and the associated motive in the Voevodsky category of motivic complexes 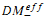 (F). We relate the motive of GL1 (A) to the motive of the Čech simplicial scheme χ, associated to the Severi-Brauer variety of A, and compute the second differential in the resulting spectral sequence for motivic cohomology.
(F). We relate the motive of GL1 (A) to the motive of the Čech simplicial scheme χ, associated to the Severi-Brauer variety of A, and compute the second differential in the resulting spectral sequence for motivic cohomology.