Refine search
Actions for selected content:
12 results
RANK JUMPS AND GROWTH OF SHAFAREVICH–TATE GROUPS FOR ELLIPTIC CURVES IN
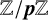 ${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1-38
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding the Iwasawa invariants of Selmer groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1390-1422
- Print publication:
- October 2021
-
- Article
- Export citation
ON THE SELMER GROUP OF A CERTAIN
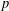 $p$-ADIC LIE EXTENSION
$p$-ADIC LIE EXTENSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 245-255
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Growth of
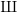 $\unicode[STIX]{x0428}$ in towers for isogenous curves
$\unicode[STIX]{x0428}$ in towers for isogenous curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 1981-2005
- Print publication:
- November 2015
-
- Article
- Export citation
Growth of Selmer Groups of CM Abelian Varieties
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 3 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 654-666
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
Selmer groups and class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 416-434
- Print publication:
- March 2015
-
- Article
- Export citation
ON POSITIVE PROPORTION OF RANK-ZERO TWISTS OF ELLIPTIC CURVES OVER
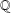 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 07 November 2014, pp. 281-288
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Weil–Châtelet divisible elements in Tate–Shafarevich groups I: The Bashmakov problem for elliptic curves over
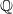 $ \mathbb{Q} $
$ \mathbb{Q} $
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 729-753
- Print publication:
- May 2013
-
- Article
- Export citation
Tate–Shafarevich groups in anticyclotomic ℤp-extensions at supersingular primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 19 February 2009, pp. 293-308
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
CENTRES OF SKEWFIELDS AND COMPLETELY FAITHFUL IWASAWA MODULES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 3 / July 2008
- Published online by Cambridge University Press:
- 18 March 2008, pp. 457-468
- Print publication:
- July 2008
-
- Article
- Export citation
On the two-variable Iwasawa main conjecture
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 5 / September 2006
- Published online by Cambridge University Press:
- 25 September 2006, pp. 1157-1200
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Galois Theory for the Selmer Group of an Abelian Variety
-
- Journal:
- Compositio Mathematica / Volume 136 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 255-297
- Print publication:
- May 2003
-
- Article
-
- You have access
- Export citation
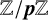
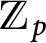
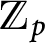
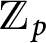
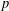
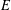
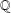
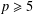
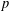
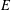
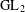
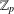
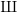
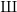
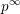
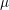
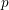
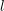
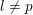
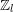
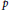
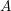
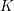
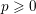
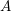
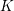
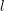
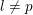
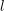
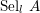
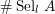
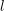
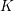
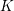
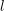
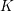
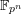
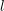
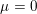
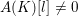
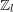
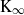 the anticyclotomic ℤ
the anticyclotomic ℤ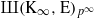 has trivial Λ-corank and, in the process, also show that
has trivial Λ-corank and, in the process, also show that 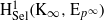 and
and  both have Λ-corank two.
both have Λ-corank two.