Refine search
Actions for selected content:
2 results
MODULES WITH FI-EXTENDING HULLS
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue 2 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 347-357
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
On a class of radicals of rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 184-192
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
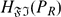 (called the absolute FI-extending hull of
(called the absolute FI-extending hull of 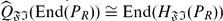 , where
, where  is the smallest right FI-extending right ring of quotients of End(
is the smallest right FI-extending right ring of quotients of End(