Refine search
Actions for selected content:
4 results
Log-normalization constant estimation using the ensemble Kalman–Bucy filter with application to high-dimensional models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1139-1163
- Print publication:
- December 2022
-
- Article
- Export citation
OPTIMAL FILTERING IN DISCRETE-TIME SYSTEMS WITH TIME DELAYS AND MARKOVIAN JUMP PARAMETERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 18 June 2010, pp. 218-233
-
- Article
-
- You have access
- Export citation
On the Phase Portrait of the Fast Filtering Algorithms
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 4 / 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 609-630
- Print publication:
- 1999
-
- Article
- Export citation
Integral Comparison Theorems for Scalar Riccati Equations and Applications
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 1 / 01 March 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 82-97
- Print publication:
- 01 March 1982
-
- Article
-
- You have access
- Export citation
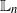
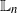
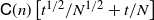
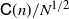
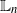

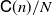
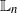
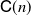
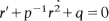 and (2)
and (2) 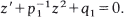 . The comparisons are of an integral type and involve an auxiliary function μ. Applications are given to disconjugacy theory for self-adjoint equations of the second and fourth order.
. The comparisons are of an integral type and involve an auxiliary function μ. Applications are given to disconjugacy theory for self-adjoint equations of the second and fourth order.