No CrossRef data available.
Article contents
Integral Comparison Theorems for Scalar Riccati Equations and Applications
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Comparison theorems are developed for the pair of first order Riccati equations (1) 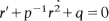 and (2)
and (2) 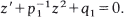 . The comparisons are of an integral type and involve an auxiliary function μ. Applications are given to disconjugacy theory for self-adjoint equations of the second and fourth order.
. The comparisons are of an integral type and involve an auxiliary function μ. Applications are given to disconjugacy theory for self-adjoint equations of the second and fourth order.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982
References
1.
Butler, G. J., Hille-Wintner comparison theorems for second order ordinary differential equations, Proc. Amer. Math. Soc.
76 (1979), 51-59.Google Scholar
2.
Elias, U., Oscillatory solutions and extremal points for a linear differential equation, Arch. Rational Mech. Anal.
71 (1979), 177-198.Google Scholar
3.
Erbe, L., Hille-Wintner comparison theorems for self-adjoint fourth order linear differential equations, Proc. Amer. Math. Soc, 80 (1980), All-All.Google Scholar
6.
Howard, H. C., Oscillation criteria for fourth order linear differential equations, Trans. Amer. Math. Soc.
96 (1960), 296-311.Google Scholar
7.
Jones, R. A., Comparison theorems for matrix Riccati equations, SIAM J. Appl. Math.
29 (1975), 77-90.Google Scholar
8.
Leighton, W. and Nehari, Z.. On the oscillation of solutions of self-adjoint linear differential equations of the fourth order, Trans. Amer. Math. Soc.
89 (1958), 325-377.Google Scholar
9.
Levin, A.Ju
A comparison principle for second order differential equation. Soviet Math. Dokl.
1 (1961), 1313-1316.Google Scholar
10.
Stafford, R. A. and Heidel, J. W., A new comparison theorem for scalar Riccati equation, Bull. Amer. Math. Soc.
80 (1974), 754-757.Google Scholar
11.
Swanson, C. A., Comparison and oscillation theory for linear differential equation, Academic Press, New York, 1968.Google Scholar
12.
Travis, C. C., On the comparison theorem for scalar Riccati equation, Proc. Amer. Math. Soc.
52 (1975), 311-314.Google Scholar
13.
Wintner, A., On the comparison theorem of Kneser-Hille, math. Scand.
5 (1957), 255-260.Google Scholar
14.
Wong, J. S. W., Oscillation and nonoscillation of solutions of second order linear differential equations with integrable coefficients, Trans. Amer. Math. Soc.
144 (1969), 197-215.Google Scholar

