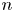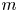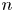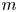Refine search
Actions for selected content:
60 results
Optimal asset allocation and reinsurance problem under enhanced dynamic contagion processes
-
- Journal:
- Annals of Actuarial Science , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strategies for offering an m-out-of-n policy for multi-peril catastrophe insurance
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 26 September 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Risk, Uncertainty, and the Demand for Political Innovation
-
- Book:
- Insuring States in an Uncertain World
- Published online:
- 13 August 2025
- Print publication:
- 18 September 2025, pp 7-19
-
- Chapter
-
- You have access
- HTML
- Export citation
Introduction: Insurance, Then and Now
-
- Book:
- Insuring States in an Uncertain World
- Published online:
- 13 August 2025
- Print publication:
- 18 September 2025, pp 1-6
-
- Chapter
-
- You have access
- HTML
- Export citation

Insuring States in an Uncertain World
- Towards the Collaborative Government of Complex Risks
-
- Published online:
- 13 August 2025
- Print publication:
- 18 September 2025
Utilizing large language models (LLMs) for quantitative reasoning-intensive tasks within the (re)insurance sector
-
- Journal:
- Annals of Actuarial Science , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinite-horizon Fuk–Nagaev inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1076-1088
- Print publication:
- September 2025
-
- Article
- Export citation
Bad decisions have consequences: how cyber security could fall victim to climate change
-
- Journal:
- British Actuarial Journal / Volume 30 / 2025
- Published online by Cambridge University Press:
- 21 May 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On penalized goal-reaching probability minimization under borrowing and short-selling constraints
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 05 November 2024, pp. 652-673
- Print publication:
- June 2025
-
- Article
- Export citation
Catastrophe insurance decision making when the science is uncertain
-
- Journal:
- Economics & Philosophy / Volume 41 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 11 September 2024, pp. 161-177
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Risk sharing in equity-linked insurance products: Stackelberg equilibrium between an insurer and a reinsurer
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 54 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 129-158
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bridging the gap between pricing and reserving with an occurrence and development model for non-life insurance claims
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 185-212
- Print publication:
- May 2023
-
- Article
- Export citation
Pareto-optimal reinsurance with default risk and solvency regulation
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 518-545
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On impact of largest claims reinsurance treaties on the ceding company’s loss reserve
- Part of
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 2 / July 2023
- Published online by Cambridge University Press:
- 01 February 2023, pp. 328-357
-
- Article
- Export citation
A class of non-zero-sum stochastic differential games between two mean–variance insurers under stochastic volatility
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 November 2022, pp. 491-517
-
- Article
- Export citation
16 - Risk Transfer
-
- Book:
- Quantitative Enterprise Risk Management
- Published online:
- 28 July 2022
- Print publication:
- 05 May 2022, pp 442-481
-
- Chapter
- Export citation
An adaptive strategy for offering m-out-of-n insurance policies
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 15 March 2022, pp. 106-134
-
- Article
- Export citation
Hedging the Price Risk Inherent in Revenue Protection Insurance
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 53 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 04 October 2021, pp. 510-530
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Standards to Create New Insurance Markets
-
- Book:
- The Power of Standards
- Published online:
- 04 July 2019
- Print publication:
- 11 July 2019, pp 140-172
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
AN EXTREME-VALUE THEORY APPROXIMATION SCHEME IN REINSURANCE AND INSURANCE-LINKED SECURITIES
- Part of
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 48 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 03 July 2018, pp. 1157-1173
- Print publication:
- September 2018
-
- Article
- Export citation