Refine search
Actions for selected content:
6 results
2 - Least Squares: Geometric, Algebraic, and Numerical Aspects
-
- Book:
- Mathematical Methods in Data Science
- Published online:
- 04 November 2025
- Print publication:
- 30 October 2025, pp 67-127
-
- Chapter
- Export citation
Principal Component Analysis with External Information on both Subjects and Variables
-
- Journal:
- Psychometrika / Volume 56 / Issue 1 / March 1991
- Published online by Cambridge University Press:
- 01 January 2025, pp. 97-120
-
- Article
- Export citation
A Bayesian Vector Multidimensional Scaling Procedure Incorporating Dimension Reparameterization with Variable Selection
-
- Journal:
- Psychometrika / Volume 80 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1043-1065
-
- Article
- Export citation
4 - Matrices
-
- Book:
- Numerical Methods in Physics with Python
- Published online:
- 30 August 2023
- Print publication:
- 20 July 2023, pp 126-231
-
- Chapter
- Export citation
2 - Algebraic Eigenproblems and Their Applications
- from Part I - Matrix Methods
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 64-154
-
- Chapter
- Export citation
A NOTE ON COMPUTING THE INTERSECTION OF SPHERES IN
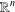 $\mathbb{R}^{n}$
$\mathbb{R}^{n}$
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 November 2017, pp. 271-279
-
- Article
-
- You have access
- Export citation