Refine search
Actions for selected content:
3 results
‘COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 12 January 2015, pp. 351-352
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 254-265
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
WHEN IS THE AUTOMORPHISM GROUP OF A VIRTUALLY POLYCYCLIC GROUP VIRTUALLY POLYCYCLIC?
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 10 September 2003, pp. 527-533
- Print publication:
- September 2003
-
- Article
-
- You have access
- Export citation
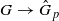 induces an isomorphism
induces an isomorphism 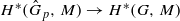 for any discrete
for any discrete 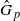 -module
-module 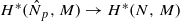 is an isomorphism for any discrete
is an isomorphism for any discrete 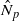 -module
-module 