Refine search
Actions for selected content:
2 results
Some constructions of modular forms for the Weil representation of SL2(ℤ)
-
- Journal:
- Nagoya Mathematical Journal / Volume 220 / December 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-43
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On generalized theta series liftings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-238
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
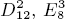 and to the Leech lattice.
and to the Leech lattice.