Refine search
Actions for selected content:
9 results
Analysis of Multiple Partially Ordered Responses to Belief Items with Don’t Know Option
-
- Journal:
- Psychometrika / Volume 81 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 01 January 2025, pp. 483-505
-
- Article
- Export citation
On the cross-product conjecture for the number of linear extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 535-562
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Metric monads
-
- Journal:
- Mathematical Structures in Computer Science / Volume 31 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 10 September 2021, pp. 535-552
-
- Article
-
- You have access
- Open access
- Export citation
On the Dual König Property of the Order-interval Hypergraph of Two Classes of N-free Posets
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 43-53
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
q-analogues of Ehrhart polynomials
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 339-358
-
- Article
- Export citation
FROM A1 TO D5: TOWARDS A FORCING-RELATEDCLASSIFICATION OF RELATIONAL STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 279-295
- Print publication:
- March 2014
-
- Article
- Export citation
Some Algebraic Properties of Machine Poset of Infinite Words
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 3 / July 2008
- Published online by Cambridge University Press:
- 03 June 2008, pp. 451-466
- Print publication:
- July 2008
-
- Article
- Export citation
Algebraic and graph-theoretic propertiesofinfinite n-posets
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 305-322
- Print publication:
- January 2005
-
- Article
- Export citation
Compact generation in partially ordered sets
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 69-83
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation





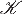 and relate it to finitary enriched monads over
and relate it to finitary enriched monads over