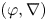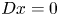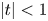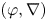Refine search
Actions for selected content:
2 results
Higher Chow cycles on a family of Kummer surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Logarithmic growth filtrations for
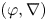 $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1265-1301
- Print publication:
- June 2021
-
- Article
- Export citation