Refine search
Actions for selected content:
5 results
EXPLICIT SOLUTIONS FOR CONTINUOUS-TIME QBD PROCESSES BY USING RELATIONS BETWEEN MATRIX GEOMETRIC ANALYSIS AND THE PROBABILITY GENERATING FUNCTIONS METHOD
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 03 January 2020, pp. 565-580
-
- Article
- Export citation
Bonferroni inequalities and deviations of discrete distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-121
- Print publication:
- March 1996
-
- Article
- Export citation
Sums of i.i.d. random variables and an application to the explosion criterion for markov branching processes
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue 1 / March 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 29-38
- Print publication:
- March 1982
-
- Article
- Export citation
Series expansions of probability generating functions and bounds for the extinction probability of a branching process
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 4 / December 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 939-947
- Print publication:
- December 1980
-
- Article
- Export citation
Polynomial bounds for probability generating functions
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 3 / September 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-514
- Print publication:
- September 1975
-
- Article
- Export citation
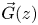
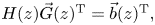
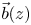
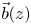
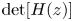
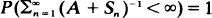 in terms of
in terms of 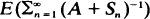 , where
, where 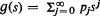 by a polynomial
by a polynomial 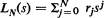 is considered. It is shown that if the coefficients
is considered. It is shown that if the coefficients 