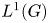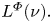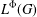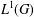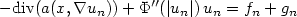Refine search
Actions for selected content:
7 results
Convolution structures for an Orlicz space with respect to vector measures on a compact group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 87-98
-
- Article
- Export citation
AMENABILITY AND ORLICZ FIGÀ-TALAMANCA HERZ ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 218-229
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
17 - Probabilistic Tools II
- from Part 2 - Advanced Toolbox
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 435-472
-
- Chapter
- Export citation
Exponential models by Orlicz spaces and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 682-700
- Print publication:
- September 2018
-
- Article
- Export citation
A CONVOLUTION-INDUCED TOPOLOGY ON THE ORLICZ SPACE OF A LOCALLY COMPACT GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 19 January 2015, pp. 1-11
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Orlicz capacities and applications to some existence questions for elliptic pdes having measure data
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 9 / January 2003
- Published online by Cambridge University Press:
- 15 September 2003, pp. 317-341
- Print publication:
- January 2003
-
- Article
- Export citation
Orlicz Spaces Without Strongly Extreme Points and Without H-Points
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 2 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-177
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation