Refine search
Actions for selected content:
2 results
Non-monotone waves of a stage-structured SLIRM epidemic model with latent period
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1407-1442
- Print publication:
- October 2021
-
- Article
- Export citation
Error Analysis for a Non-Monotone FEM for a Singularly Perturbed Problem with Two Small Parameters
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 10 March 2015, pp. 196-206
- Print publication:
- April 2015
-
- Article
- Export citation
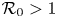

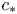
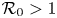
 (
(