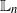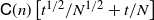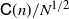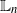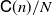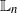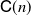Refine search
Actions for selected content:
4 results
Fitting and Testing Log-Linear Subpopulation Models with Known Support
-
- Journal:
- Psychometrika / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 01 January 2025, pp. 917-939
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - The Conway–Maxwell–Poisson (COM–Poisson) Distribution
-
- Book:
- The Conway–Maxwell–Poisson Distribution
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 22-70
-
- Chapter
- Export citation
Log-normalization constant estimation using the ensemble Kalman–Bucy filter with application to high-dimensional models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1139-1163
- Print publication:
- December 2022
-
- Article
- Export citation
An LCFS finite buffer model with finite source batch input
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 2 / June 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 372-380
- Print publication:
- June 1989
-
- Article
- Export citation